题目内容
【再读教材】
宽与长的比是
或
(约为0.618)的矩形叫做黄金矩形.
下面,我们用宽为4cm的矩形纸片折叠一个黄金矩形.
第一步,在矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平.
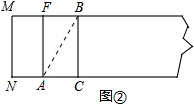
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
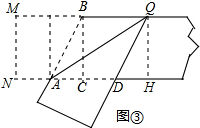
第三步,折出内侧矩形的对角线AB,并把它折到图③中所示的AD处.
第四步,展平纸片,按照所得的D点折出DE,如图④…
【问题解决】
(1)图③中AB=
(2)你发现图④中有几个黄金矩形?请都写出来,并选择其中一个说明理由;
(3)在图③中,连接BD,以AQ、BD为两直角边作直角三角形,求该直角三角形斜边的长.
宽与长的比是
| ||
| 2 |
| 2 | ||
|
下面,我们用宽为4cm的矩形纸片折叠一个黄金矩形.

第一步,在矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步,折出内侧矩形的对角线AB,并把它折到图③中所示的AD处.
第四步,展平纸片,按照所得的D点折出DE,如图④…
【问题解决】
(1)图③中AB=
2
| 5 |
2
cm(保留根号);| 5 |
(2)你发现图④中有几个黄金矩形?请都写出来,并选择其中一个说明理由;
(3)在图③中,连接BD,以AQ、BD为两直角边作直角三角形,求该直角三角形斜边的长.
分析:(1)连接AB,由折叠的性质,可得AC=2,在Rt△ABC中,利用勾股定理可求出AB的长度.
(2)首先求出CD=2
-2,ND=2
+2,再由黄金矩形的定义即可作出判断.
(3)过点Q作QH⊥ND于点H,由tan∠QDH=tan∠ABM,可求出DH的长度,继而得出AH的长度,在Rt△AHQ中利用勾股定理求出AQ,继而可利用勾股定理可求出该直角三角形斜边的长.
(2)首先求出CD=2
| 5 |
| 5 |
(3)过点Q作QH⊥ND于点H,由tan∠QDH=tan∠ABM,可求出DH的长度,继而得出AH的长度,在Rt△AHQ中利用勾股定理求出AQ,继而可利用勾股定理可求出该直角三角形斜边的长.
解答:解:(1)∵四边形MNCB是正方形,
∴NC=MN=4cm,
由折叠的性质得:AC=
NC=2cm,
连接AB,如图②:
在Rt△ABC中,AB=
=
=2
;
(2)图④中的黄金矩形有:矩形BCDE,矩形MNDE;
∵AD=2
,AN=AC=2,
∴CD=2
-2,ND=2
+2,
∴
=
=
,
故矩形BCDE是黄金矩形;
∴
=
=
,
故矩形MNDE是黄金矩形.
(3)过点Q作QH⊥ND于点H,如图③所示:
由折叠的性质可得:∠ADQ=∠ABQ,
∴∠QDH=∠ABM,
∴tan∠QDH=tan∠ABM=
=
=
,
∴DH=2,
∴AH=AD+DH=2
+2,
在Rt△AQH中,AQ2=AH2+QH2=(2
+2)2+16=40+8
,
BD2=CD2+BC2=(2
-2)2+16=40-8
,
以AQ、BD为两直角边作直角三角形,则该直角三角形斜边长=
=
=4
.
∴NC=MN=4cm,
由折叠的性质得:AC=
| 1 |
| 2 |
连接AB,如图②:

在Rt△ABC中,AB=
| AC2+BC2 |
| 22+42 |
| 5 |
(2)图④中的黄金矩形有:矩形BCDE,矩形MNDE;
∵AD=2
| 5 |
∴CD=2
| 5 |
| 5 |
∴
| CD |
| BC |
2
| ||
| 4 |
| ||
| 2 |
故矩形BCDE是黄金矩形;
∴
| MN |
| ND |
| 4 | ||
2
|
| 2 | ||
|
故矩形MNDE是黄金矩形.
(3)过点Q作QH⊥ND于点H,如图③所示:

由折叠的性质可得:∠ADQ=∠ABQ,
∴∠QDH=∠ABM,
∴tan∠QDH=tan∠ABM=
| 4 |
| 2 |
| QH |
| DH |
| 4 |
| DH |
∴DH=2,
∴AH=AD+DH=2
| 5 |
在Rt△AQH中,AQ2=AH2+QH2=(2
| 5 |
| 5 |
BD2=CD2+BC2=(2
| 5 |
| 5 |
以AQ、BD为两直角边作直角三角形,则该直角三角形斜边长=
| AQ2+BD2 |
| 80 |
| 5 |
点评:本题考查了几何变换的综合,涉及了折叠的性质、勾股定理、锐角三角函数的定义,综合考察的知识点较多,解答本题需要我们具有扎实的基本功,数形结合,灵活解答.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目