题目内容
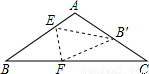
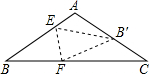 已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是________.
已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是________.
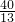
分析:首先由折叠的性质得到BF=B′F;再由相似三角形的判定(对应边成比例的三角形相似),可得BF的长.注意此题没指明对应边,需分类讨论.
解答:由题意得:BF=B′F,∠C=∠C,
若
 =
= ,
,则△CB′F∽△CAB,
设BF=x,则FC=BC-BF=8-x,
∴
 ,
,解得:x=
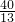 ;
;若
 ,
,
则△CB′F∽△CBA,
设BF=y,则FC=BC-BF=8-y,
∴
 ,
,解得:y=4.
∵此时CB′=6.5>5,
即B′不在AC上,舍去;
∴BF的长为
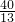 .
.故答案为:
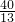 .
.点评:此题考查了相似三角形的判定与性质.注意此题没说明这两个三角形的对应边,所以需要分类讨论,解题是要小心别漏解.

练习册系列答案
相关题目
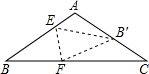 已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是
已知三角形纸片(△ABC)中,AB=AC=5,BC=8,将三角形按照如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是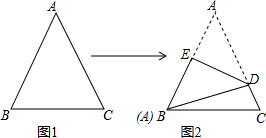 如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,求∠DBC的大小.
如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,求∠DBC的大小.