题目内容
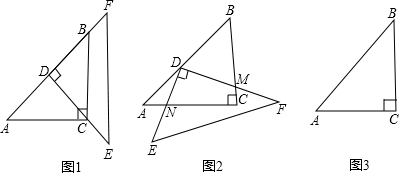
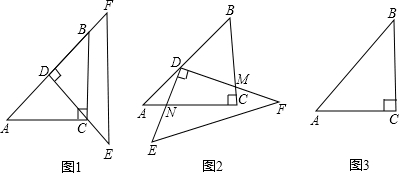
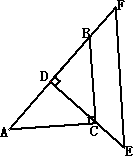
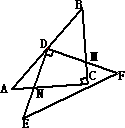
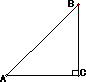
(1)已知:有两块完全相同的含45°角的三角板,如图1,将Rt△DEF的直角顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的______;(2)如图2,点D不动,将Rt△DEF绕着顶点D旋转α(0°<∠α<90°),这时两块三角板重叠部分为任意四边形DNCM,这时四边形DNCM的面积是△ABC的面积的______;
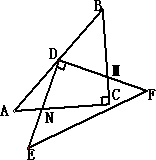
(3)若Rt△DEF的顶点D在AB上移动(不与点A、B重合),且两条直角边与Rt△ABC的两条直角边相交,是否存在一点,使得两块三角板重叠部分的面积是Rt△ABC的面积的
 ?如果存在,请在图3中画出此时的图形,并说明点D在AB上的位置;如果不存在,说明理由.
?如果存在,请在图3中画出此时的图形,并说明点D在AB上的位置;如果不存在,说明理由.
【答案】分析:(1)D为AB的中点,S△ABC= AB×CD,S△DBC=
AB×CD,S△DBC= BD×CD,即可得出;
BD×CD,即可得出;
(2)连接CD,易证△CDM≌△ADN,四边形DNCM的面积等于△ACD的面积,结合(1)即可得出;
(3)取DF⊥BC,DE⊥AC,则四边形DNCM是矩形,设AB=a,BD=x,则DM=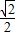 x,DN=
x,DN= (a-x),AC=BC=
(a-x),AC=BC= a,分别表示出S△ABC和S矩形DNCM,利用其面积比,即可求出D的位置.
a,分别表示出S△ABC和S矩形DNCM,利用其面积比,即可求出D的位置.
解答:解:(1)∵在直角△ABC中,D为斜边AB的中点,
∴AD=BD=CD= AB,CD⊥AB,
AB,CD⊥AB,
∵S△ABC= AB×CD,S△DBC=
AB×CD,S△DBC= BD×CD,
BD×CD,
∴S△DBC= S△ABC
S△ABC
故答案为 .
.
(2)如图,连接CD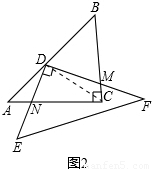 ,
,
∵∠ADN+∠NDC=∠CDM+∠NDC,
∴∠ADN=∠CDM,
又∵∠A=∠DCB,AD=CD,
∴△ADN≌△CDM,
∴S四边形DNCM=S△ADC,
∴S四边形DNCM= S△ABC;
S△ABC;
故答案为 .
.
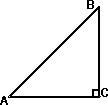
(3)如图,DF⊥BC,DE⊥AC,则四边形DNCM是矩形 ;
;
设AB=a,BD=x,
∴DM=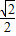 x,DN=
x,DN=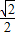 (a-x),AC=BC=
(a-x),AC=BC=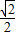 a,
a,
∴S△ABC= ×
× a×
a× a=
a= a2,
a2,
S矩形DNCM= x×
x× (a-x)=
(a-x)= (ax-x2),
(ax-x2),
∴ =
= ,
,
整理得,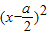 =
= ,
,
∴x1= a,x2=
a,x2= a,
a,
∴点D在B点 或
或 处时,两块三角板重叠部分的面积是Rt△ABC的面积的
处时,两块三角板重叠部分的面积是Rt△ABC的面积的 .
.
点评:本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质,(3)中取四边形是矩形,是解答的关键,思考问题的角度是从特殊到一般.
 AB×CD,S△DBC=
AB×CD,S△DBC= BD×CD,即可得出;
BD×CD,即可得出;(2)连接CD,易证△CDM≌△ADN,四边形DNCM的面积等于△ACD的面积,结合(1)即可得出;
(3)取DF⊥BC,DE⊥AC,则四边形DNCM是矩形,设AB=a,BD=x,则DM=
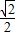 x,DN=
x,DN= (a-x),AC=BC=
(a-x),AC=BC= a,分别表示出S△ABC和S矩形DNCM,利用其面积比,即可求出D的位置.
a,分别表示出S△ABC和S矩形DNCM,利用其面积比,即可求出D的位置.解答:解:(1)∵在直角△ABC中,D为斜边AB的中点,
∴AD=BD=CD=
 AB,CD⊥AB,
AB,CD⊥AB,∵S△ABC=
 AB×CD,S△DBC=
AB×CD,S△DBC= BD×CD,
BD×CD,∴S△DBC=
 S△ABC
S△ABC故答案为
 .
.(2)如图,连接CD
 ,
,∵∠ADN+∠NDC=∠CDM+∠NDC,
∴∠ADN=∠CDM,
又∵∠A=∠DCB,AD=CD,
∴△ADN≌△CDM,
∴S四边形DNCM=S△ADC,
∴S四边形DNCM=
 S△ABC;
S△ABC;故答案为
 .
.(3)如图,DF⊥BC,DE⊥AC,则四边形DNCM是矩形
 ;
;设AB=a,BD=x,
∴DM=
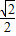 x,DN=
x,DN=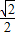 (a-x),AC=BC=
(a-x),AC=BC=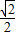 a,
a,∴S△ABC=
 ×
× a×
a× a=
a= a2,
a2,S矩形DNCM=
 x×
x× (a-x)=
(a-x)= (ax-x2),
(ax-x2),∴
 =
= ,
,整理得,
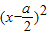 =
= ,
,∴x1=
 a,x2=
a,x2= a,
a,∴点D在B点
 或
或 处时,两块三角板重叠部分的面积是Rt△ABC的面积的
处时,两块三角板重叠部分的面积是Rt△ABC的面积的 .
.点评:本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质,(3)中取四边形是矩形,是解答的关键,思考问题的角度是从特殊到一般.

练习册系列答案
相关题目

 ?如果存在,请在图3中画出此时的图形,并说明点D在AB上的位置;如果不存在,说明理由.
?如果存在,请在图3中画出此时的图形,并说明点D在AB上的位置;如果不存在,说明理由.