题目内容
为了美化社区环境，某小区准备对门口的一块矩形空地ABCD重新进行绿化，已知矩形的边长AB=10m，BC=20m，绿化方案如下：在矩形ABCD中间的一块四边形EFGH地面上种花，剩下的其它四块地面上铺设草坪，并要AH=CF=2AE=2CG．在满足上述条件的所有设计中，求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积．
【答案】分析：先设AE=x，根据图形，可知S四边形EFGH=S矩形-S△BEF-S△DGH-S△AEH-S△GFC，由已知条件及矩形性质可得：△BEF≌△DGH，△AEH≌△CGF，即S四边形EFGH=S矩形-2S△BEF-2S△AEH=-4（x-5）2+100．因为0＜x＜10，故x=5，S有最大值．
解答：解：设AE=x，则AH=CF=2x，BE=DC=10-x，BF=DH=20-2x，
∴四边形EFGH的面积S=10×20-2×
x•2x-2×
（10-x）（20-2x），
即S=-4x2+40x，
又∵S=-4（x-5）2+100，
由题意，得0＜x＜10，而0＜5＜10，
∴当AE=5m时，四边形EFGH的面积最大，最大面积是100m2．
点评：本题利用了全等的三角形面积相等，以及矩形的性质，二次函数求最大值的问题．
解答：解：设AE=x，则AH=CF=2x，BE=DC=10-x，BF=DH=20-2x，
∴四边形EFGH的面积S=10×20-2×
x•2x-2×（10-x）（20-2x），即S=-4x2+40x，
又∵S=-4（x-5）2+100，
由题意，得0＜x＜10，而0＜5＜10，
∴当AE=5m时，四边形EFGH的面积最大，最大面积是100m2．
点评：本题利用了全等的三角形面积相等，以及矩形的性质，二次函数求最大值的问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
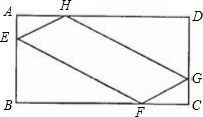为了美化社区环境，某小区准备对门口的一块矩形空地ABCD重新进行绿化，已知矩形的边长AB=10m，BC=20m，绿化方案如下：在矩形ABCD中间的一块四边形EFGH地面上种花，剩下的其它四块地面上铺设草坪，并要AH=CF=2AE=2CG．在满足上述条件的所有设计中，求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积．
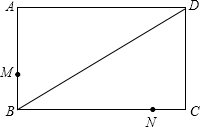（2012•鞍山）如图，某社区有一矩形广场ABCD，在边AB上的M点和边BC上的N点分别有一棵景观树，为了进一步美化环境，社区欲在BD上（点B除外）选一点P再种一棵景观树，使得∠MPN=90°，请在图中利用尺规作图画出点P的位置（要求：不写已知、求证、作法和结论，保留作图痕迹）．
为了美化社区环境，某小区准备对门口的一块矩形空地ABCD重新进行绿化，已知矩形的边长AB=10m，BC=20m，绿化方案如下：在矩形ABCD中间的一块四边形EFGH地面上种花，剩下的其它四块地面上铺设草坪，并要AH=CF=2AE=2CG．在满足上述条件的所有设计中，求出使四边形EFGH面积最大的AE的长和此时四边形EFGH的面积．