题目内容
已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= .
2525
试题分析:仔细分析所给式子的特征可得a1+a2+a3+…a100= (a1+a2)+(a3+a4)+…+(a99+a100),再代入求值,根据从1开始的相邻奇数的和即可求得结果.
由题意得a1+a2+a3+…a100= (a1+a2)+(a3+a4)+…+(a99+a100)=1+3+5+…+99=2525.
点评:解答本题的关键是读懂所给式子的规律,再根据这个规律解题即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
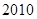 年
年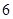 月
月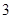 日,人类首次模拟火星载人航天飞行试验 “火星-500”正式启动.包括中国志愿者王跃在内的
日,人类首次模拟火星载人航天飞行试验 “火星-500”正式启动.包括中国志愿者王跃在内的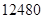 小时的 “火星之旅”.将
小时的 “火星之旅”.将


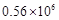
 , ,第2009个数是 。
, ,第2009个数是 。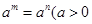 且
且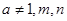 是正整数,则
是正整数,则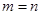 )你能利用上面的结论解决下面的2个问题吗?试试看,相信你一定行!
)你能利用上面的结论解决下面的2个问题吗?试试看,相信你一定行!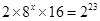 ,求
,求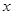 的值;
的值;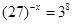 ,求
,求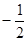 ,
, ,-3,
,-3, 。
。