题目内容
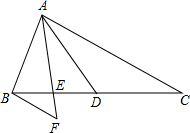 (2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
(2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.(1)求证:AC=3BF;
(2)如果AE=
| 3 |
分析:(1)根据平行线分线段成比例定理由BF∥AC得BF:AC=BE:EC,再利用BD=CD,BE=DE,得CE=3BE,于是即可得到结论;
(2)由AE=
ED得AE2=3ED2,把CE=3ED代入得AE2=CE•ED,即AE:ED=CE:AE,根据相似三角形的判定易得△AED∽△CEA,则AD:AC=ED:AE,用EB代替ED即可得到结论.
(2)由AE=
| 3 |
解答:证明:(1)∵BF∥AC,
∴BF:AC=BE:EC,
又∵BD=CD,BE=DE,
∴CE=3BE,
∴AC=3BF;
(2)∵AE=
ED,
∴AE2=3ED2,
又∵CE=3ED,
∴AE2=CE•ED,即AE:ED=CE:AE,
而∠AED=∠CEA,
∴△AED∽△CEA,
∴AD:AC=ED:AE,
又∵ED=BE,
∴AD:AC=BE:AE,
∴AD•AE=AC•BE.
∴BF:AC=BE:EC,
又∵BD=CD,BE=DE,
∴CE=3BE,
∴AC=3BF;
(2)∵AE=
| 3 |
∴AE2=3ED2,
又∵CE=3ED,
∴AE2=CE•ED,即AE:ED=CE:AE,
而∠AED=∠CEA,
∴△AED∽△CEA,
∴AD:AC=ED:AE,
又∵ED=BE,
∴AD:AC=BE:AE,
∴AD•AE=AC•BE.
点评:本题考查了相似三角形的判定与性质:如果两个三角形有两组对应边的比相等,并且这两组对应边所夹的角也相等,那么这两个三角形相似;相似三角形的对应边的比相等.也考查了平行线分线段成比例定理.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
