题目内容
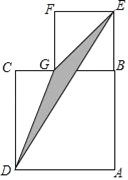
【题目】如图,正方形ABCD与正方形BEFG,且A,B,E在一直线上,已知AB=a,BE=b(b<a).
(1)用a、b的代数式表示△ADE的面积.
(2)用a、b的代数式表示△DCG的面积.
(3)用a、b的代数式表示阴影部分的面积.
【答案】(1)![]() a(a+b);(2)
a(a+b);(2)![]() b(a﹣b);(3)
b(a﹣b);(3)![]() a2+b2﹣ab.
a2+b2﹣ab.
【解析】试题分析:
(1)由S△ADE=![]() AD·(AB+BE)列式表达即可;
AD·(AB+BE)列式表达即可;
(2)由S△DCG=![]() DC·(BC-BG)列式表达即可;
DC·(BC-BG)列式表达即可;
(3)由S阴影=两个正方形的面积之和-S△ADE-S△GEF-S△CDG列式即可;
试题解析:
(1)∵四边形ABCD和四边形BEFG是正方形,AB=a,BE=b,A,B,E在一直线上,
∴AB=AD=a,∠A=90°,∠EBG=∠ABC=90°,AE=AB+BE=a+b,
∴S△ADE=![]() AD·AE=
AD·AE=![]() ;
;
(2)∵四边形ABCD和四边形BEFG是正方形,AB=a,BE=b,
∴AB=DC=BC=a,∠C=90°,BG=BE=b,
∴CG=BC-BG=a-b,
∴S△DCG=![]() DC·CG=
DC·CG=![]() ;
;
(3)∵四边形ABCD和四边形BEFG是正方形,AB=a,BE=b,
∴S正方形ABCD+S正方形BEFG=![]() .
.
又∵S△ADE=![]() ,S△DCG=
,S△DCG=![]() ,S△EFG=
,S△EFG=![]() EF·FG=
EF·FG=![]() ,
,
∴S阴影=![]() -S△ADE-S△GEF-S△CDG
-S△ADE-S△GEF-S△CDG
=![]()
=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
