题目内容
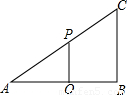
(2002•广州)如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP⊥AB交AC于点P.(1)证明线段AO、OB、OP中,任意两条线段长度之和大于第三条线段的长度;
(2)过线段OB(包括端点)上任一点M,作MN⊥AB交AC于点N.如果要使线段AM、MB、MN中任意两条线段长度之和大于第三条线段的长度,那么请求出线段AM的长度的取值范围.
【答案】分析:(1)利用相似三角形的性质求得个线段的长即可;
(2)根据相似三角形的性质得比例式,列不等式即可求得.
解答:解:(1)∵∠B=90°,OP⊥AB,
∴∠AOP=∠B=90°,
∴△AOP∽△ABC.∴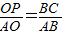
∵AB=4,BC=3,O是AB的中点.
∴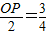
∴OP=
∵OP= <AO=OB=2,且
<AO=OB=2,且 +2>2.
+2>2.
∴OP+AB>OB
即AO,BO,OP中,任意两条线段的长度之和大于第三条线段的长度.
∵∠B=90°,OP⊥AB
∴OP∥BC
∵O是AB的中点,
∴OP是△ABC的中位线.
∴OP= BC
BC
∵BC=3
∴OP= ;
;
(2)当M在OB上时,设AM=x(2≤x≤4)
则MB=4-x,
∵△AMN∽△ABC
∴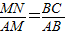
∴MN= x
x
又MN<AM,MB<AM
∴MN+MB>AM,
∴ x+(4-x)>x
x+(4-x)>x
∴x<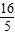
∴AM的取值范围为2≤AM< .
.
点评:此题考查了相似三角形的判定与性质、三角形三边关系,此题难度较大,解题要细心.
(2)根据相似三角形的性质得比例式,列不等式即可求得.
解答:解:(1)∵∠B=90°,OP⊥AB,
∴∠AOP=∠B=90°,
∴△AOP∽△ABC.∴
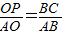
∵AB=4,BC=3,O是AB的中点.
∴
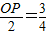
∴OP=

∵OP=
 <AO=OB=2,且
<AO=OB=2,且 +2>2.
+2>2.∴OP+AB>OB
即AO,BO,OP中,任意两条线段的长度之和大于第三条线段的长度.
∵∠B=90°,OP⊥AB

∴OP∥BC
∵O是AB的中点,
∴OP是△ABC的中位线.
∴OP=
 BC
BC∵BC=3
∴OP=
 ;
;(2)当M在OB上时,设AM=x(2≤x≤4)
则MB=4-x,
∵△AMN∽△ABC
∴
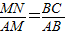
∴MN=
 x
x又MN<AM,MB<AM
∴MN+MB>AM,
∴
 x+(4-x)>x
x+(4-x)>x∴x<
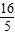
∴AM的取值范围为2≤AM<
 .
.点评:此题考查了相似三角形的判定与性质、三角形三边关系,此题难度较大,解题要细心.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目