题目内容
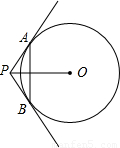
如图所示,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10cm,则弦AB的长为( )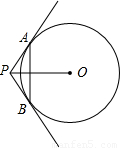
A.5
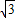 cm
cmB.5cm
C.10
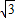 cm
cmD.
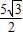 cm
cm
【答案】分析:先由题意得出△AOB为等边三角形,再根据勾股定理即可得出.
解答: 解:连OA,OB,
解:连OA,OB,
∵直线PA,PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,
∵∠APB=120°,
∴∠AOB=60°,
∵OA=OB,
则△AOB为等边三角形,
由直角三角形中30°角所对的直角边等于斜边的一半可得:
PA=5cm,
再由勾股定理OA= =5
=5 cm,
cm,
从而得AB=5 (cm).
(cm).
故选A.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
解答:
 解:连OA,OB,
解:连OA,OB,∵直线PA,PB是⊙O的两条切线,
∴OA⊥PA,OB⊥PB,
∵∠APB=120°,
∴∠AOB=60°,
∵OA=OB,
则△AOB为等边三角形,
由直角三角形中30°角所对的直角边等于斜边的一半可得:
PA=5cm,
再由勾股定理OA=
 =5
=5 cm,
cm,从而得AB=5
 (cm).
(cm).故选A.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 如图所示,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10cm,则弦AB的长为( )
如图所示,直线PA,PB是⊙O的两条切线,A,B分别为切点,∠APB=120°,OP=10cm,则弦AB的长为( )A、5
| ||||
| B、5cm | ||||
C、10
| ||||
D、
|
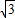 cm
cm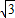 cm
cm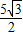 cm
cm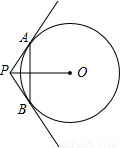
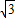 cm
cm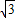 cm
cm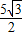 cm
cm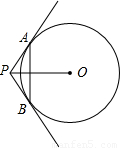
 cm
cm cm
cm cm
cm