Question

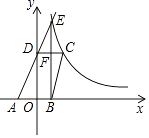
【题目】如图，已知四边形ABCD顶点A、B在x轴上，点D在y轴上，函数y= （x＞0）的图象经过点C（2，3），直线AD交双曲线于点E，并且EB⊥x轴，CD⊥y轴，EB与CD交于点F．

（1）若EB= OD，求点E的坐标；
（2）若四边形ABCD为平行四边形，求过A、D两点的函数关系式．

Answer 1

【答案】
（1）解：∵C（2，3），

把C（2，3）代入y= 中，k=6，

∴y= ，

∵CD⊥y轴，

∴OD=3，

∵BE= OD，

∴BE=4，

∴y=4时，4= ，

∴x= ，

∴点E坐标（ ，4）；

（2）解：设E（m， ），则B（m，0），

∵四边形ABCD是平行四边形，

∴CD=AB=2，

∵DF∥AB，

∴ = ，

∴ = ，

解得m=1，

∴E（1，6），

设直线AD的解析式为y=kx+b，则有 ，

解得 ，

∴直线AD的解析式为y=3x+3

【解析】（1）根据点C坐标求出反比例函数的解析式，再求出点E的纵坐标，即可解决问题．（2）设E（m， ），则B（m，0），由四边形ABCD是平行四边形，推出CD=AB=2，由DF∥AB，推出 = ，推出 = ，解得m=1，可得E（1，6），设直线AD的解析式为y=kx+b，利用待定系数法即可解决问题．
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．