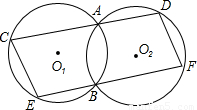
题目内容
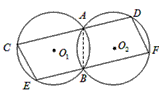
已知:如图,两个等圆⊙O1和⊙O2相交于A,B两点,经过点A的直线与两圆分别交于点C,点D,经过点B的直线与两圆分别交于点E,点F,若CD∥EF。
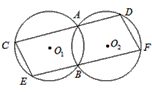
求证:(1)四边形EFDC是平行四边形;
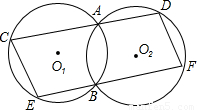
(2)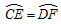 。
。
(2)
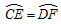 。
。| 证明:(1)连接AB, ∵ABEC是⊙O1的内接四边形, ∴∠BAD=∠E, 又∵ADFB是⊙O2的内接四边形, ∴∠BAD+∠F=180°, ∴∠E+∠F=180°, ∴CE∥DF, ∵CD∥EF, ∴四边形CEFD是平行四边形; (2)由(1)得:四边形CEFD是平行四边形, ∴CE=DF, ∴ 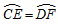 。 。 |
 |

练习册系列答案
相关题目
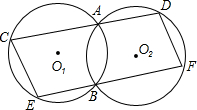 于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
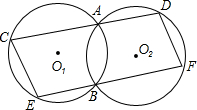
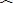
 .
.
 .
.