题目内容
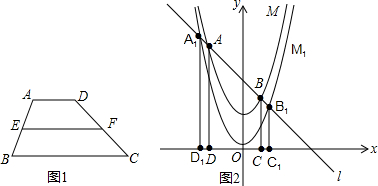
请阅读下面知识:梯形中位线的定义:梯形两腰中点的连线,叫做梯形的中位线.如图,E,F是梯形ABCD两腰AB,CD的中点,则EF是梯形的中位线梯形中位线与两底长度的关系:梯形中位线长度等于两底长的和的一半如图:EF=
 (AD+BC)利用上面的知识,完成下面题目的解答已知:直线l与抛物线M交于点A,B两点,抛物线M的对称轴为y轴,过点A,B作x轴的垂线段,垂足分别为D,C,已知A(-1,3),B(
(AD+BC)利用上面的知识,完成下面题目的解答已知:直线l与抛物线M交于点A,B两点,抛物线M的对称轴为y轴,过点A,B作x轴的垂线段,垂足分别为D,C,已知A(-1,3),B(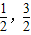 )
)(1)求梯形ABCD中位线的长度;
(2)求抛物线M的解析式;
(3)把抛物线M向下平移k个单位,得抛物线M1(抛物线M1的顶点保持在x轴的上方),与直线l的交点为A1,B1,同样作x轴的垂线段,垂足为D1,C1,问此时梯形A1B1C1D1的中位线的长度(设为h)与原来相比是否发生变化?若不变,说明理由.若有改变,求出h与k的函数关系式.
【答案】分析:(1)根据A、B两点的坐标求出AD、BC的长度,再由中位线定理求出梯形ABCD中位线的长度即可;
(2)设抛物线的解析式为y=ax2+b(a≠0),把A、B两点的坐标代入即可求出ab的值,进而得出抛物线的解析式;
(3)把直线AB的解析式同抛物线的解析式联立即可出x1、x2的表达式,再代入直线AB的解析式即可得出A1、B1的坐标,进而可得出A1D1及B1C1的长度,由中位线定理即可求出梯形A1B1C1D1的中位线的长度.
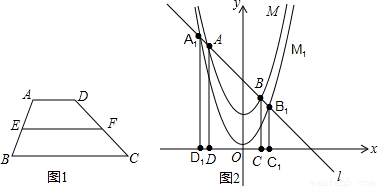
解答:解:(1)∵A(-1,3),B(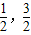 )
)
∴AD=3,BC= ,
,
∴梯形ABCD中位线= (AD+BC)=
(AD+BC)= ×(3+
×(3+ )=
)= ;
;
(2)设抛物线的解析式为y=ax2+b(a≠0),
∵点A(-1,3),B(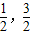 )在抛物线上,
)在抛物线上,
∴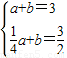 ,解得
,解得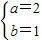 ,
,
∴抛物线的解析式为:y=2x2+1;
(3)∵抛物线M向下平移k个单位得抛物线M1,
∴抛物线M1的解析式为y=2x2+1-k,
∴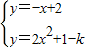 ,
,
解得x1= ,x2=
,x2= (其中x1<x2)
(其中x1<x2)
代入y=-x+2得,y1=-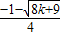 +2,y2=-
+2,y2=-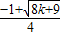 +2,
+2,
∴y1+y2=(-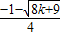 )+(-
)+(-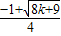 )=
)= ,
,
∴梯形A1B1C1D1的中位线长为 ,保持不变.
,保持不变.
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、梯形的中位线定理等相关知识,难度适中.
(2)设抛物线的解析式为y=ax2+b(a≠0),把A、B两点的坐标代入即可求出ab的值,进而得出抛物线的解析式;
(3)把直线AB的解析式同抛物线的解析式联立即可出x1、x2的表达式,再代入直线AB的解析式即可得出A1、B1的坐标,进而可得出A1D1及B1C1的长度,由中位线定理即可求出梯形A1B1C1D1的中位线的长度.
解答:解:(1)∵A(-1,3),B(
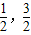 )
)∴AD=3,BC=
 ,
,∴梯形ABCD中位线=
 (AD+BC)=
(AD+BC)= ×(3+
×(3+ )=
)= ;
;(2)设抛物线的解析式为y=ax2+b(a≠0),
∵点A(-1,3),B(
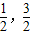 )在抛物线上,
)在抛物线上,∴
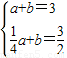 ,解得
,解得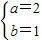 ,
,∴抛物线的解析式为:y=2x2+1;
(3)∵抛物线M向下平移k个单位得抛物线M1,
∴抛物线M1的解析式为y=2x2+1-k,
∴
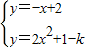 ,
,解得x1=
 ,x2=
,x2= (其中x1<x2)
(其中x1<x2)代入y=-x+2得,y1=-
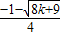 +2,y2=-
+2,y2=-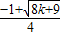 +2,
+2,∴y1+y2=(-
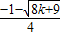 )+(-
)+(-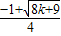 )=
)= ,
,∴梯形A1B1C1D1的中位线长为
 ,保持不变.
,保持不变.点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、梯形的中位线定理等相关知识,难度适中.

练习册系列答案
相关题目