题目内容
【题目】已知![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,下列三个命题:①若
的图象上,下列三个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③过
;③过![]() 、
、![]() 两点的直线与
两点的直线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,则
,则![]() .其中真命题个数是( )
.其中真命题个数是( )
A.0B.1C.2D.3
【答案】D
【解析】
将点A、B的坐标代入反比例函数解析式中即可判断①;然后利用反比例函数的增减性即可判断②;设![]() ,直线CD的解析式为y=ax+b,然后利用待定系数法求出直线CD的解析式,从而求出点C和点D的坐标,然后根据点A、B的位置分类讨论,分别画出对应的图形,根据三角形的面积公式即可判断③.
,直线CD的解析式为y=ax+b,然后利用待定系数法求出直线CD的解析式,从而求出点C和点D的坐标,然后根据点A、B的位置分类讨论,分别画出对应的图形,根据三角形的面积公式即可判断③.
解:将A、B的坐标代入![]() 中,得
中,得
![]() ,
,![]()
变形可得![]()
若![]()
∴![]() =
=![]() ,故①正确;
,故①正确;
∵![]() >0,x>0
>0,x>0
∴反比例函数图象在第一象限,y随x的增大而减小
∵当![]() <
<![]() ,
,
∴![]() ,故②正确;
,故②正确;
设![]() ,直线CD的解析式为y=ax+b,
,直线CD的解析式为y=ax+b,
∴反比例函数的解析式为![]()
∴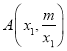 、
、 ,
,
将点A、B的坐标代入y=ax+b中,得
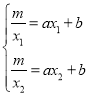
解得: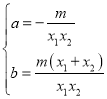
∴直线CD的解析式为![]()
当x=0时,y=![]() ;当y=0时,x=
;当y=0时,x=![]()
∴点D的坐标为(0,![]() ),点C的坐标为(
),点C的坐标为(![]() ,0)
,0)
当点B在点A左侧时,过点B作BE⊥y轴于E,过点A作AF⊥x轴于F,如下图所示
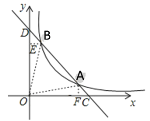
∴AF=![]() ,BE=
,BE=![]() ,OC=
,OC=![]() ,OD=
,OD=![]()
∴S△AOC=![]() OC·AF=
OC·AF=![]()
![]() ·
·![]() =
=![]()
S△BOD=![]() OD·BE=
OD·BE=![]() ·
·![]() ·
·![]() =
=![]()
∴S△AOC= S△BOD;
当点B在点A右侧时,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,如下图所示
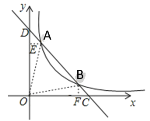
∴BF=![]() ,AE=
,AE=![]() ,OC=
,OC=![]() ,OD=
,OD=![]()
∴S△AOD=![]() OD·AE=
OD·AE=![]() ·
·![]() ·
·![]() =
=![]()
S△BOC=![]() OC·BF=
OC·BF=![]() ·
·![]() ·
·![]() =
=![]()
∴S△AOD= S△BOC
∴S△AOD+S△AOB= S△BOC+S△AOB
∴S△AOC= S△BOD,故③正确.
综上:正确的有结论有3个
故选D.

【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
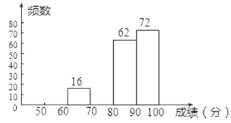
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
【题目】如图,A,B,C为⊙O上的定点.连接AB,AC,M为AB上的一个动点,连接CM,将射线MC绕点M顺时针旋转90°,交⊙O于点D,连接BD.若AB=6cm,AC=2cm,记A,M两点间距离为xcm,B,D两点间的距离为ycm.
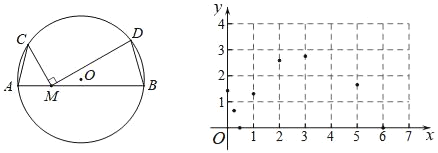
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表,补全表格:
x/cm | 0 | 0.25 | 0.47 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 1.43 | 0.66 | 0 | 1.31 | 2.59 | 2.76 |
| 1.66 | 0 |
(2)在平面直角坐标系xOy中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BD=AC时,AM的长度约为 cm.