题目内容
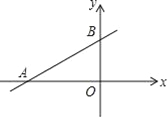
【题目】如图，已知函数y=
x+
的图象与x轴交于点A，与y轴交于点B，点P是x轴上一点，若△PAB为等腰三角形，则点P的坐标不可能是（ ）
A. （﹣3﹣2，0） B. （3，0） C. （﹣1，0） D. （2
，0）
【答案】D
【解析】如下图所示：
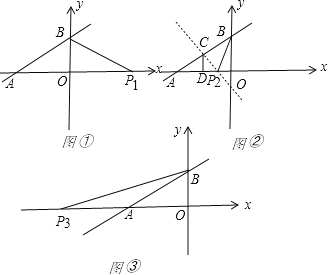
∵函数y=
的图象与x轴交于点A，与y轴交于点B，
在y=
中,令y=0可得x=3,令x=0可得y=
，
∴A(3,0),B(0, 
)，
∴AB=
，
(1)当AB=BP时,点P与
重合,则 
(3,0)；
(2)当AP=BP时,点P与点
重合，如图②所示：
过AB的中点C作x轴的垂线，垂足为D，
由题意知： 
=ADPD，
∵点C的坐标为(
,
),设点P的坐标为(a,0)
∴
=(
+3)(a+3)
解之得：a=1
即：点P的坐标为(1,0)
(3)当AB=AP时,点
重合,则P3(32
,0)
综上所述：若△PAB为等腰三角形,则点P的坐标可能是(3,0)、(1,0)、(32
,0)
故选D.
练习册系列答案
相关题目
【题目】为了更好地迎接庐阳区排球比赛，某校积极准备，从全校学生中遴选出21名同学进行相应的排球训练，该训练队成员的身高如下表：
身高（cm） | 170 | 172 | 175 | 178 | 180 | 182 | 185 |
人数（个） | 2 | 4 | 5 | 2 | 4 | 3 | 1 |
则该校排球队21名同学身高的众数和中位数分别是（单位：cm）（ ）
A. 185，178B. 178，175C. 175，178D. 175，175
【题目】如图，在△ABC中，AB=AC,∠BAC=64°，∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上，F在AC上)折叠，点C与点O恰好重合，则∠OEC为_________度．
