Question

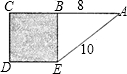如图，阴影部分是正方形，则四边形ACDE的面积为

1. A.
   146
2. B.
   76
3. C.
   84
4. D.
   60

Answer 1

D
分析：要求四边形ACDE的面积，只需求出底边DE、AC及高BE的长，即变为求正方形BCDE的边长，根据图形，正方形有一边是一个直角三角形的边，由勾股定理可以求出．
解答：如图，设正方形的边长为xcm，
由勾股定理得：BE²+AB²=AE²，即x²+8²=10²，
解得x=6，
∴AC=AB+BC=14，DE=6，BE=6，
所以：四边形ACDE的面积为（6+14）×6=60cm²．
故选D．
点评：本题主要考查勾股定理及梯形的面积公式，比较容易解答，根据勾股定理求出正方形的边长是关键．