题目内容
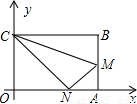
(2010•鄂尔多斯)如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.(1)求N点、M点的坐标;
(2)将抛物线y=x2-36向右平移a(0<a<10)个单位后,得到抛物线l,l经过点N,求抛物线l的解析式;
(3)①抛物线l的对称轴上存在点P,使得P点到M、N两点的距离之差最大,求P点的坐标;
②若点D是线段OC上的一个动点(不与O、C重合),过点D作DE∥OA交CN于E,设CD的长为m,△PDE的面积为S,求S与m之间的函数关系式,并说明S是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
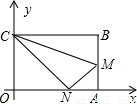
【答案】分析:(1)根据折叠的性质知:BC=CN=OA,由此可在Rt△OCN中用勾股定理求出ON的长(由此可求出N点的坐标),即可得到NA的值;在Rt△AMN中,用AM表示出MN、BM的值,然后由勾股定理即可求出AM的长,也就得到了M点的坐标;
(2)用a表示出抛物线l的解析式,然后将N点坐标代入其中,即可求出抛物线l的解析式;
(3)①此题的关键是确定P点的位置,若PM-PN最大,那么P点必为直线MN与抛物线对称轴的交点(可由三角形三边关系定理推出),可用待定系数法求出直线MN的解析式,联立抛物线的对称轴方程,即可得到P点的坐标;
②由于DE∥ON,易证得△CDE∽△CON,根据相似三角形得到的比例线段即可求出DE的表达式,以DE为底,P、D纵坐标差的绝对值为高即可得到△DEP的面积,由此可求出关于S、m的函数关系式,根据所得函数的性质及自变量的取值范围即可求出S的最大值及对应的m的值.
解答: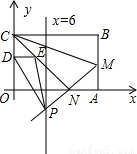 解:如图
解:如图
(1)∵CN=CB=15,OC=9,
∴ON=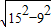 =12,
=12,
∴N(12,0);
又∵AN=OA-ON=15-12=3,
设AM=x
∴32+x2=(9-x)2
∴x=4,M(15,4);
(2)解法一:设抛物线l为y=(x-a)2-36
则(12-a)2=36
∴a1=6或a2=18(舍去)
∴抛物线l:y=(x-6)2-36
解法二:
∵x2-36=0,
∴x1=-6,x2=6;
∴y=x2-36与x轴的交点为(-6,0)或(6,0)
由题意知,交点(6,0)向右平移6个单位到N点,
所以y=x2-36向右平移6个单位得到抛物线l:y=(x-6)2-36;
(3)①由“三角形任意两边的差小于第三边”知:P点是直线MN与对称轴x=6的交点,
设直线MN的解析式为y=kx+b,
则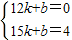 ,
,
解得 ,
,
∴y= x-16,
x-16,
∴P(6,-8);
②∵DE∥OA,
∴△CDE∽△CON,
∴ ;
;
∴S=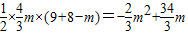
∵a=- <0,开口向下,又m=-
<0,开口向下,又m=-
∴S有最大值,且S最大=-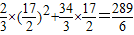 .
.
点评:此题考查了勾股定理、二次函数解析式的确定、函数图象的平移、图形面积的求法、三角形三边关系定理以及相似三角形的判定和性质,综合性强,难度偏大.
(2)用a表示出抛物线l的解析式,然后将N点坐标代入其中,即可求出抛物线l的解析式;
(3)①此题的关键是确定P点的位置,若PM-PN最大,那么P点必为直线MN与抛物线对称轴的交点(可由三角形三边关系定理推出),可用待定系数法求出直线MN的解析式,联立抛物线的对称轴方程,即可得到P点的坐标;
②由于DE∥ON,易证得△CDE∽△CON,根据相似三角形得到的比例线段即可求出DE的表达式,以DE为底,P、D纵坐标差的绝对值为高即可得到△DEP的面积,由此可求出关于S、m的函数关系式,根据所得函数的性质及自变量的取值范围即可求出S的最大值及对应的m的值.
解答:
 解:如图
解:如图(1)∵CN=CB=15,OC=9,
∴ON=
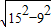 =12,
=12,∴N(12,0);
又∵AN=OA-ON=15-12=3,
设AM=x
∴32+x2=(9-x)2
∴x=4,M(15,4);
(2)解法一:设抛物线l为y=(x-a)2-36
则(12-a)2=36
∴a1=6或a2=18(舍去)
∴抛物线l:y=(x-6)2-36
解法二:
∵x2-36=0,
∴x1=-6,x2=6;
∴y=x2-36与x轴的交点为(-6,0)或(6,0)
由题意知,交点(6,0)向右平移6个单位到N点,
所以y=x2-36向右平移6个单位得到抛物线l:y=(x-6)2-36;
(3)①由“三角形任意两边的差小于第三边”知:P点是直线MN与对称轴x=6的交点,
设直线MN的解析式为y=kx+b,
则
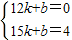 ,
,解得
 ,
,∴y=
 x-16,
x-16,∴P(6,-8);
②∵DE∥OA,
∴△CDE∽△CON,
∴
 ;
;∴S=
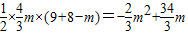
∵a=-
 <0,开口向下,又m=-
<0,开口向下,又m=-
∴S有最大值,且S最大=-
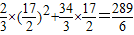 .
.点评:此题考查了勾股定理、二次函数解析式的确定、函数图象的平移、图形面积的求法、三角形三边关系定理以及相似三角形的判定和性质,综合性强,难度偏大.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
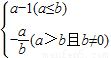 ,则函数y=3※x的图象大致是( )
,则函数y=3※x的图象大致是( )