题目内容
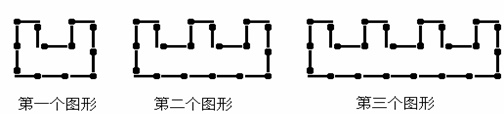
25、用火柴棒按下列方式搭建三角形:

(1)填表:

(2)当三角形的个数为n时,火柴棒的根数为
(3)求当n=1000时,火柴棒的根数是多少?
(4)按照上述方法,能否用100根火柴棒搭建三角形?如果能,请求出n;如果不能,请简述理由.

(1)填表:

(2)当三角形的个数为n时,火柴棒的根数为
2n+1
.(用n的代数式表示)(3)求当n=1000时,火柴棒的根数是多少?
(4)按照上述方法,能否用100根火柴棒搭建三角形?如果能,请求出n;如果不能,请简述理由.
分析:(1)画出三角形个数为1、2、3、4、5的图形,数出火柴棒的根数填入表中即可.
(2)由表格可以看出火柴棒的递增规律,由此可得出火柴棒的根数的表达式.
(3)将n=1000时代入(2)的表示式,即可得到火柴棒的根数.
(4)设火柴棒根数为s,将s=100代入(2)的表达式,求解n是整数则可搭建三角形,不是则不能.
(2)由表格可以看出火柴棒的递增规律,由此可得出火柴棒的根数的表达式.
(3)将n=1000时代入(2)的表示式,即可得到火柴棒的根数.
(4)设火柴棒根数为s,将s=100代入(2)的表达式,求解n是整数则可搭建三角形,不是则不能.
解答:解:(1)填表:

(2)观察(1)中的表格,火柴棒根数以3为公差递增,故当三角形的个数为n时,火柴棒的根数为2n+1(表格(1分),填空2分)
(3)当n=1000时
2n+1=2×1000+1=2001;(5分)
即求当n=1000时,火柴棒的根数是2001根.
(4)设火柴棒根数为s,将s=100代入(2)的表示式,即
2n+1=100,解得,n=49.5
不是整数,故不能搭建三角形.

(2)观察(1)中的表格,火柴棒根数以3为公差递增,故当三角形的个数为n时,火柴棒的根数为2n+1(表格(1分),填空2分)
(3)当n=1000时
2n+1=2×1000+1=2001;(5分)
即求当n=1000时,火柴棒的根数是2001根.
(4)设火柴棒根数为s,将s=100代入(2)的表示式,即
2n+1=100,解得,n=49.5
不是整数,故不能搭建三角形.
点评:本题主要涉及图形的变化规律,难度中等.注意由特殊到一般的归纳方法.

练习册系列答案
相关题目