题目内容
【题目】已知正方形ABCD中,点E、F分别为边AB、BC上的点,连接CE、DF相交于点G,CE=DF.
(1)如图①,求证:DF⊥CE;
(2)如图②,连接BD,取BD的中点O,连接OE、OF、EF,求证:△OEF为等腰直角三角形
(3)如图③,在(2)的条件下,将△CBE和△DCF分别沿CB、DC翻折到△CBM和△DCN的位置,连接OM、ON、MN,若AE=2BE,ON=![]() ,求EG的长.
,求EG的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)如图1中,证明Rt△CBE≌△Rt△DCF(HL),即可解决问题.
(2)如图2中,连接OC.想办法证明△OBE≌△OCF(SAS),即可解决问题.
(3)如图3中,连接OC.设BE=a,则BM=EB=CF=CN=a,AE=2a,BC=AB=3a,首先证明△OMN是等腰直角三角形,利用勾股定理求出a即可解决问题.
(1)如图1中,

∵四边形ABCD是正方形,
∴BC=CD,∠B=∠DCF=90°,
∵DE=CE,
∴Rt△CBE≌△Rt△DCF(HL),
∴BE=CF,∠ECB=∠CDF,
∵∠ECB+∠DCE=90°,
∴∠CDF+∠DCE=90°,
∴∠CGD=90°,
∴EC⊥DF.
(2)如图2中,连接OC.
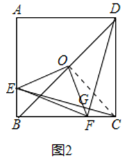
∵CB=CD,∠BCD=90°,OB=OD,
∴OC=OB=OD,OC⊥BD,
∴∠OCB=45°,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∴∠OBE=∠OCF,
∵BE=CF,OB=OC,
∴△OBE≌△OCF(SAS),
∴OE=OF,∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△EOF是等腰直角三角形.
(3)如图3中,连接OC.设BE=a,则BM=EB=CF=CN=a,AE=2a,BC=AB=3a,

∵BE=BM,CF=CN,BE=CF,
∴BM=CN,
∵OB=OC,∠OBM=∠OCN=135°,BM=CN,
∴△OBM≌△OCN(SAS),
∴∠BOM=∠COM,
∴∠MON=∠BOC=90°,
∴△MON是等腰直角三角形,
∵OM=ON=![]() ,
,
∴MN=2![]() ,
,
在Rt△MBN中,a2+16a2=68,
∴a=2(负根已经舍弃),
BE=2,BC=6,EC=2![]() ,
,
∵△CGF∽△CBE,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.







