题目内容
(2009•厦门)我们知道,当一条直线与一个圆有两个公共点时,称这条直线与这个圆相交.类似地,我们定义:当一条直线与一个正方形有两个公共点时,称这条直线与这个正方形相交.如图,在平面直角坐标系中,正方形OABC的顶点为O(0,0)、A(1,0)、B(1,1)、C(0,1).
(1)判断直线y=
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;(2)设d是点O到直线y=-
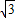 x+b的距离,若直线y=-
x+b的距离,若直线y=-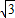 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.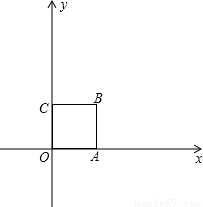
【答案】分析:(1)直线AB的解析式是x=1,直线BC的解析式是y=1,求出这两条直线与直线y= x+
x+ 的交点,判断交点是否在正方形的边上,就可以判断;
的交点,判断交点是否在正方形的边上,就可以判断;
(2)当直线y=-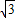 x+b经过点B时,直线与正方形只有一个公共点,可以求出d的值,当直线在B的下方,在经过O点的直线的上方时,直线与正方形相交.
x+b经过点B时,直线与正方形只有一个公共点,可以求出d的值,当直线在B的下方,在经过O点的直线的上方时,直线与正方形相交.
解答:解:(1)相交.
∵直线y= x+
x+ 与线段OC交于点(0,
与线段OC交于点(0, ),同时直线y=
),同时直线y= x+
x+ 与线段CB交于点(
与线段CB交于点( ,1),
,1),
∴直线y= x+
x+ 与正方形OABC相交;
与正方形OABC相交;
(2)当直线y=- x+b经过点B时,
x+b经过点B时,
即有1=- +b,
+b,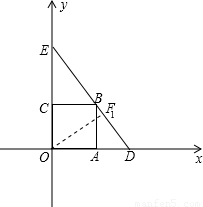
∴b=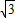 +1.
+1.
即y=-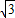 x+1+
x+1+ ,
,
记直线y=-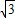 x+1+
x+1+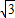 与x、y轴的交点分别为D、E,
与x、y轴的交点分别为D、E,
则D( ,0),E(0,1+
,0),E(0,1+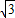 ),
),
解法1:在Rt△BAD中,tan∠BDA=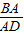 =
=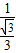 =
=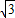 ,
,
∴∠EDO=60°,∠OED=30度,
过O作OF1⊥DE,垂足为F1,则OF1=d1,
在Rt△OF1E中,
∵∠OED=30°,
∴d1=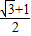 ;
;
法2:∴DE= (3+
(3+ ),
),
过O作OF1⊥DE,垂足为F1,则OF1=d1,
∴d1=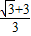 ×(1+
×(1+ )÷
)÷ (3+
(3+ )=
)=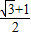 ,
,
∵直线y=-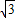 x+b与直线y=-
x+b与直线y=-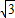 x+1+
x+1+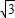 平行,
平行,
法1:当直线y=-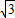 x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O、B重合.
x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O、B重合.
故直线y=-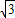 x+b也一定与线段OF1相交,记交点为F,则F不与点O、F1重合,且OF=d,
x+b也一定与线段OF1相交,记交点为F,则F不与点O、F1重合,且OF=d,
∴当直线y=- x+b与正方形相交时,
x+b与正方形相交时,
有0<d< ;
;
法2:当直线y=-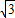 x+b与直线y=x(x>0)相交时,
x+b与直线y=x(x>0)相交时,
有x=-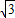 x+b,即x=
x+b,即x= ,
,
当0<b<1+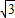 时,0<x<1,0<y<1,
时,0<x<1,0<y<1,
此时直线y=-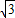 x+b与线段OB相交,且交点不与点O、B重合;
x+b与线段OB相交,且交点不与点O、B重合;
当b>1+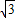 时,x>1,
时,x>1,
此时直线y=- x+b与线段OB不相交.
x+b与线段OB不相交.
而当b≤0时,直线y=-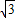 x+b不经过第一象限,即与正方形OABC不相交.
x+b不经过第一象限,即与正方形OABC不相交.
∴当0<b<1+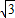 时,d随b的增大而增大,则直线y=-
时,d随b的增大而增大,则直线y=- x+b与正方形OABC相交,
x+b与正方形OABC相交,
此时有0<d<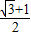 .
.
点评:本题主要考查了待定系数法求函数解析式,正确确定直线与正方形相交的位置是解决本题的关键.
 x+
x+ 的交点,判断交点是否在正方形的边上,就可以判断;
的交点,判断交点是否在正方形的边上,就可以判断;(2)当直线y=-
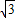 x+b经过点B时,直线与正方形只有一个公共点,可以求出d的值,当直线在B的下方,在经过O点的直线的上方时,直线与正方形相交.
x+b经过点B时,直线与正方形只有一个公共点,可以求出d的值,当直线在B的下方,在经过O点的直线的上方时,直线与正方形相交.解答:解:(1)相交.
∵直线y=
 x+
x+ 与线段OC交于点(0,
与线段OC交于点(0, ),同时直线y=
),同时直线y= x+
x+ 与线段CB交于点(
与线段CB交于点( ,1),
,1),∴直线y=
 x+
x+ 与正方形OABC相交;
与正方形OABC相交;(2)当直线y=-
 x+b经过点B时,
x+b经过点B时,即有1=-
 +b,
+b,
∴b=
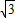 +1.
+1.即y=-
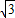 x+1+
x+1+ ,
,记直线y=-
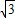 x+1+
x+1+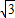 与x、y轴的交点分别为D、E,
与x、y轴的交点分别为D、E,则D(
 ,0),E(0,1+
,0),E(0,1+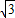 ),
),解法1:在Rt△BAD中,tan∠BDA=
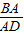 =
=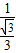 =
=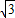 ,
,∴∠EDO=60°,∠OED=30度,
过O作OF1⊥DE,垂足为F1,则OF1=d1,
在Rt△OF1E中,
∵∠OED=30°,
∴d1=
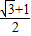 ;
;法2:∴DE=
 (3+
(3+ ),
),过O作OF1⊥DE,垂足为F1,则OF1=d1,
∴d1=
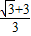 ×(1+
×(1+ )÷
)÷ (3+
(3+ )=
)=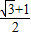 ,
,∵直线y=-
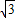 x+b与直线y=-
x+b与直线y=-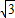 x+1+
x+1+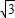 平行,
平行,法1:当直线y=-
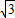 x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O、B重合.
x+b与正方形OABC相交时,一定与线段OB相交,且交点不与点O、B重合.故直线y=-
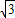 x+b也一定与线段OF1相交,记交点为F,则F不与点O、F1重合,且OF=d,
x+b也一定与线段OF1相交,记交点为F,则F不与点O、F1重合,且OF=d,∴当直线y=-
 x+b与正方形相交时,
x+b与正方形相交时,有0<d<
 ;
;法2:当直线y=-
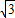 x+b与直线y=x(x>0)相交时,
x+b与直线y=x(x>0)相交时,有x=-
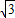 x+b,即x=
x+b,即x= ,
,当0<b<1+
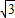 时,0<x<1,0<y<1,
时,0<x<1,0<y<1,此时直线y=-
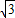 x+b与线段OB相交,且交点不与点O、B重合;
x+b与线段OB相交,且交点不与点O、B重合;当b>1+
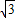 时,x>1,
时,x>1,此时直线y=-
 x+b与线段OB不相交.
x+b与线段OB不相交.而当b≤0时,直线y=-
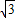 x+b不经过第一象限,即与正方形OABC不相交.
x+b不经过第一象限,即与正方形OABC不相交.∴当0<b<1+
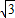 时,d随b的增大而增大,则直线y=-
时,d随b的增大而增大,则直线y=- x+b与正方形OABC相交,
x+b与正方形OABC相交,此时有0<d<
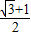 .
.点评:本题主要考查了待定系数法求函数解析式,正确确定直线与正方形相交的位置是解决本题的关键.

练习册系列答案
相关题目
 x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由;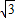 x+b的距离,若直线y=-
x+b的距离,若直线y=-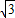 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.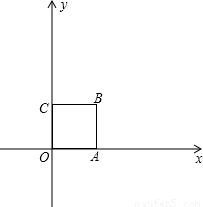
 ≤OP≤2+
≤OP≤2+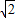 时,试判断直线DE与抛物线y=x2-x+c+
时,试判断直线DE与抛物线y=x2-x+c+ 的交点个数,并说明理由.
的交点个数,并说明理由.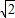 ≤OP≤2+
≤OP≤2+ 时,试判断直线DE与抛物线y=x2-x+c+
时,试判断直线DE与抛物线y=x2-x+c+ 的交点个数,并说明理由.
的交点个数,并说明理由. x+
x+ 与正方形OABC是否相交,并说明理由;
与正方形OABC是否相交,并说明理由; x+b的距离,若直线y=-
x+b的距离,若直线y=-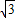 x+b与正方形OABC相交,求d的取值范围.
x+b与正方形OABC相交,求d的取值范围.