题目内容
已知:非零实数a,b,c满足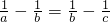 ,求证:ab+bc=2ac.
,求证:ab+bc=2ac.
证明:∵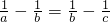 ,
,
∴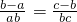 ,
,
∴c(b-a)=a(c-b),
∴bc-ac=ac-ab,
∴ab+bc=2ac.
分析:先把等式两边分别通分,再把分式化为整式后移项,合并同类项即可得到结果.
点评:本题根据分式证明等式的相等,不过还是考查分式的加减运算.
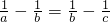 ,
,∴
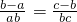 ,
,∴c(b-a)=a(c-b),
∴bc-ac=ac-ab,
∴ab+bc=2ac.
分析:先把等式两边分别通分,再把分式化为整式后移项,合并同类项即可得到结果.
点评:本题根据分式证明等式的相等,不过还是考查分式的加减运算.

练习册系列答案
相关题目
 +|-3|-2tan60°+
+|-3|-2tan60°+ ;
;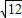 +|-3|-2tan60°+
+|-3|-2tan60°+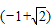 ;
;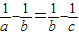 ,求证:ab+bc=2ac.
,求证:ab+bc=2ac. ,求证:ab+bc=2ac.
,求证:ab+bc=2ac.