题目内容
(本题满分9分)
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当 很大时,摸到白球的频率将会接近 (精确到0.01);
很大时,摸到白球的频率将会接近 (精确到0.01);
(2)假如你摸一次,你摸到黑球的概率P(黑球)= ;
(3)试估算盒子里白、黑两种颜色的球各有多少个?
(4)在(2)条件下如果要使摸到白球的概率为 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
【答案】
解:(1)0.55 ;(2)0.45, …………………………………………………2分
(3)40×0.55=22,40-22=18, ………………………………………………………3分
盒子里白、黑两种颜色的球分别约有22个和18个. ………………………………4分
(4)设需要往盒子里再放入x个白球,…………………………………………………5分
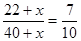 …………………………………………………………………………6分
…………………………………………………………………………6分
解得,x=20,………………………………………………………………………7分
经检验x=20是原方程的根. ……………………………………………………………8分
所以需要往盒子里再放入20个白球. ……………………………………………………9分
【解析】略

练习册系列答案
相关题目


 ,得到黄球的概率为
,得到黄球的概率为 ,得到绿球的概率为
,得到绿球的概率为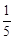 .已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
.已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
 (1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km; (2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?