题目内容
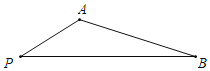
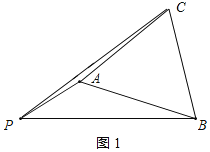
【题目】已知PA=2,PB=4![]() ,以AB为边作等边△ABC,使P、C落在直线AB的两侧,连接PC.
,以AB为边作等边△ABC,使P、C落在直线AB的两侧,连接PC.
(1)如图,当∠APB=30°时,
①按要求补全图形;②求AB和PC的长.
(2)当∠APB变化时,其它条件不变,则PC的最大值为 ,此时∠APB= .
【答案】(1)①详见解析;②AB=2![]() ,PC=2
,PC=2![]() ;(2)2+4
;(2)2+4![]() ,120°.
,120°.
【解析】
(1)①按要求补全图形即可;
②作AH⊥PB于H,在Rt△APH中,由直角三角形的性质得出PH=![]() PA=1,由勾股定理得出PH=
PA=1,由勾股定理得出PH=![]() ,得出BH=3
,得出BH=3![]() ,在Rt△AHB中,由勾股定理得AB=2
,在Rt△AHB中,由勾股定理得AB=2![]() ;再由旋转的性质和勾股定理求出P'B,即可得出PC的长;
;再由旋转的性质和勾股定理求出P'B,即可得出PC的长;
(2)把△PAC绕点A顺时针旋转60°得到△P'AB,根据旋转的性质得AP'=AP=2,P'B=PC,∠P'AP=60°,得出△APP'为等边三角形,得出PP'=PA=2,∠APP'=60°,当P'点在直线PB上时,P'B最大,得出P'B的最大值,即可得出PC的最大值,此时∠APB=120°.
(1)①补全图形,如图1所示:
②作AH⊥BP于H,如图2所示:

在Rt△APH中,∵∠APB=30°,
∴AH=![]() PA=1,
PA=1,
∴PH=![]() =
=![]() ,
,
∴BH=PB﹣PH=3![]() ,
,
在Rt△AHB中,AB=![]() =2
=2![]() ,
,
把△PAC绕点A顺时针旋转60°得△P'AB,连接PP',如图3所示:
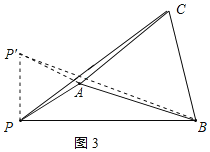
则∠APP'=60°,AP'=AP,PC=P'B,
∴△APP'是等边三角形,
∴PP'=PA=2,
∵∠APB=30°,
∴∠BPP'=90°,
∴P'B=![]() =2
=2![]() ,
,
∴PC=2![]() ;
;
(2)把△PAC绕点A顺时针旋转60°得到△P'AB,
则AP'=AP=2,P'B=PC,∠P'AP=60°,
∴△APP'为等边三角形,
∴PP'=PA=2,∠APP'=60°,
当P'点在直线PB上时,如图4所示:

此时P'B最大,最大值为2+4![]() ,
,
∴PC的最大值为2+4![]() ,此时∠APB=120°;
,此时∠APB=120°;
故答案为:2+4![]() ,120°.
,120°.

 名校课堂系列答案
名校课堂系列答案【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.