题目内容
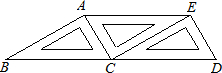
 9、如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )
9、如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有( )分析:在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答:解:∠B=∠DCE,则AB∥EC(同位角相等,两直线平行);
∠BCA=∠CAE,则AE∥DB(内错角相等,两直线平行);
∠ACE=∠DEC,则AC∥DE(内错角相等,两直线平行).
互相平行的线有:AE∥DB,AB∥EC,AC∥DE,共三组.
故选B.
∠BCA=∠CAE,则AE∥DB(内错角相等,两直线平行);
∠ACE=∠DEC,则AC∥DE(内错角相等,两直线平行).
互相平行的线有:AE∥DB,AB∥EC,AC∥DE,共三组.
故选B.
点评:本题是考查平行线的判定的基础题,比较容易.同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有
如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有