题目内容
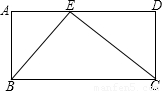
在一块长为8、宽为
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是________．
2
分析：设AE边为x，则DE边为8-x，根据相似三角形对应边成比例，列出比例式求解即可．
解答：根据题意，截出的三角形是相似三角形，
设AE=x，则DE边为8-x，
∵△ABE∽△DEC，
∴
，
即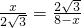
，
整理得x2-8x+12=0，
解得x1=2，x2=6（舍去），
因此较短直角边的长为2．
故应填2．
点评：本题主要利用相似三角形对应边成比例的性质，熟练掌握性质并灵活运用是解题的关键．
分析：设AE边为x，则DE边为8-x，根据相似三角形对应边成比例，列出比例式求解即可．
解答：根据题意，截出的三角形是相似三角形，
设AE=x，则DE边为8-x，
∵△ABE∽△DEC，
∴
，即
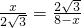，整理得x2-8x+12=0，
解得x1=2，x2=6（舍去），
因此较短直角边的长为2．
故应填2．
点评：本题主要利用相似三角形对应边成比例的性质，熟练掌握性质并灵活运用是解题的关键．
练习册系列答案
相关题目
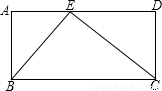
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是 ．
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是 ．
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是 ．
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是 ．
的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是 ．