题目内容
【题目】试说明:用15块大小是4×1的矩形地砖和一块大小是2×2的正方形地砖能不能恰好铺盖一块大小是8×8的正方形地面.
【答案】见解析.
【解析】
这也是一种密铺问题,从面积来看,15块4×1的矩形地砖和一块2×2的正方形地砖的面积之和为4×15+2×2=64,恰好等于8×8.从每个拼接点来看,90°×4=360°,但是这些地砖不能敲碎,不能改成面积更小的地砖.因此只考查面积和拼接点的角度之和,不能解决问题.
解:如图,在大小是8×8的正方形地面上画出64个小方格,并按如图所示的方法涂上黑,白两种颜色,黑,白小方格各有32个,每一横行或每一纵行都分别有4个黑方格和4个白方格,用一块大小是4×1的矩形地砖无论铺在横行,还是纵行上,总是盖住2个黑方格和2个白方格,铺下15块后,共能盖住30个黑方格和30个白方格,
地面上,一定剩下2个黑方格和2个白方格必须用2×2的正方形地砖,但从图中可以发现,2×2的正方形地砖无论铺在地面上的什么位置,都不能盖住2个黑方格和2个白方格,盖住的方格是3黑1白或1黑3白,
因此不能恰好铺盖成功.


练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
【题目】已知抛物线y=(x﹣1)2﹣1.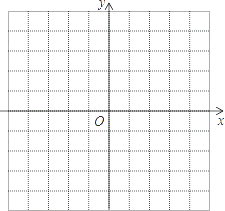
(1)该抛物线的对称轴是 , 顶点坐标;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线的图象;
x | … | … | |||||
y | … | … |
(3)根据图象,直接写出当y<0时,x的取值范围.








