Question

【题目】如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与三个正方形的面积和的比值为【 】

A. B. 1 C. D.

Answer 1

【答案】A

【解析】由题意知：三个正方形的共用顶点即为圆的圆心，也是等边三角形的重心；可设等边三角形的边长为2x，作等边三角形的高，再根据三角形重心的性质即可得到正方形的对角线的长；进而可求得等边三角形和正方形的面积，即可得到它们的面积比．
解：如图，设圆的圆心为O，过A作AD⊥BC于于D，则AD必过点O，且AO=2OD；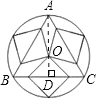

设△ABC的边长为2x，则BD=x, ， ,
∴正方形的边长为，面积为，三个正方形的面积和为,
△ABC的面积为,
∴等边三角形与三个正方形的面积和的比值为.
故选A.
“点睛”本题考查的是等边三角形及正方形的性质、三角形重心的性质找到等边三角形和正方形边长的比例关系是解答本题的关键．