题目内容
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
【答案】C
【解析】解:∵四边形ABCD是正方形,
∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,
在△ABD和△BCD中, ,
,
∴△ABD≌△BCD,
∵AD∥BC,
∴∠MDO=∠M′BO,
在△MOD和△M′OB中, ,
,
∴△MDO≌△M′BO,同理可证△NOD≌△N′OB,∴△MON≌△M′ON′,
∴全等三角形一共有4对.
故选C.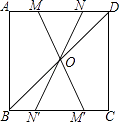
可以判断△ABD≌△BCD,△MDO≌△M′BO,△NOD≌△N′OB,△MON≌△M′ON′由此即可对称结论.本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定方法,属于基础题,中考常考题型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目






