题目内容
已知平面上四点A(0,0),B(10,0),C(12,6),D(2,6),直线y=mx-3m+6将四边形ABCD分成面积相等的两部分,则m的值为
- A.

- B.-1
- C.2
- D.

B
分析:根据点的坐标先判定出四边形ABCD是平行四边形,再根据过平行四边形中心的直线把平行四边形分成面积相等的两部分,求出中心点的坐标,然后代入直线解析式进行计算即可求解.
解答:如图,∵A(0,0),B(10,0),C(12,6),D(2,6),
∴AB=10-0=10,CD=12-2=10,
又点C、D的纵坐标相同,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵12÷2=6,6÷2=3,
∴对角线交点P的坐标是(6,3),
∵直线y=mx-3m+6将四边形ABCD分成面积相等的两部分,
∴直线y=mx-3m+6经过点P,
∴6m-3m+6=3,
解得m=-1.
故选B.
点评:本题主要考查了一次函数与平行四边形的判定,熟知过平行四边形中心的直线把平行四边形分成面积相等的两部分是解本题的关键.
分析:根据点的坐标先判定出四边形ABCD是平行四边形,再根据过平行四边形中心的直线把平行四边形分成面积相等的两部分,求出中心点的坐标,然后代入直线解析式进行计算即可求解.
解答:如图,∵A(0,0),B(10,0),C(12,6),D(2,6),

∴AB=10-0=10,CD=12-2=10,
又点C、D的纵坐标相同,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵12÷2=6,6÷2=3,
∴对角线交点P的坐标是(6,3),
∵直线y=mx-3m+6将四边形ABCD分成面积相等的两部分,
∴直线y=mx-3m+6经过点P,
∴6m-3m+6=3,
解得m=-1.
故选B.
点评:本题主要考查了一次函数与平行四边形的判定,熟知过平行四边形中心的直线把平行四边形分成面积相等的两部分是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
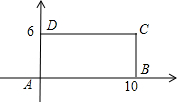 已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为
已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为 9、已知平面上四点A、B、C、D,如图:
9、已知平面上四点A、B、C、D,如图: