题目内容
根据有理数的除法符号法则“两数相除,同号得正,异号得负”,求不等式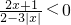 的解集.
的解集.
解:依题意得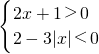 或
或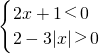 ,
,
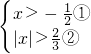 或
或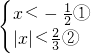 ,
,
解得第一个不等式组中的②得:x> 或x<-
或x<- ,与①取公共解集得:x>
,与①取公共解集得:x> ;
;
解得第二个不等式组中的②得:- <x<
<x< ,与①取公共解集得:-
,与①取公共解集得:- <x<-
<x<- ,
,
所以原不等式的解集为: 或
或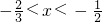 .
.
分析:根据有理数的除法符号法则“两数相除,同号得正,异号得负”,把所求的不等式转化为分子分母异号,即分子大于0且分母小于0或分子小于0且分母大于0,分别求出两不等式组的解集即可得到原不等式的解集.
点评:此题考查学生掌握有理数的除法法则,考查了转化的思想,同时考查了一元一次不等式组的解法,是一道综合题.
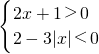 或
或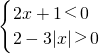 ,
,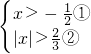 或
或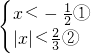 ,
,解得第一个不等式组中的②得:x>
 或x<-
或x<- ,与①取公共解集得:x>
,与①取公共解集得:x> ;
;解得第二个不等式组中的②得:-
 <x<
<x< ,与①取公共解集得:-
,与①取公共解集得:- <x<-
<x<- ,
,所以原不等式的解集为:
 或
或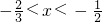 .
.分析:根据有理数的除法符号法则“两数相除,同号得正,异号得负”,把所求的不等式转化为分子分母异号,即分子大于0且分母小于0或分子小于0且分母大于0,分别求出两不等式组的解集即可得到原不等式的解集.
点评:此题考查学生掌握有理数的除法法则,考查了转化的思想,同时考查了一元一次不等式组的解法,是一道综合题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 的解集.
的解集.