题目内容
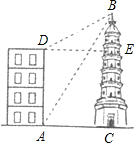 如图,小明想测量塔BC的高度.他在楼底A处测得塔顶B的仰角为60°;爬到楼顶D处测得大楼AD的高度为18米,同时测得塔顶B的仰角为30°,求塔BC的高度.
如图,小明想测量塔BC的高度.他在楼底A处测得塔顶B的仰角为60°;爬到楼顶D处测得大楼AD的高度为18米,同时测得塔顶B的仰角为30°,求塔BC的高度.
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△DBE、△ABC,应利用其中DE=AC的等量关系,进而可求出答案.
解答:解:如图,设BE=x米.
在Rt△BDE中,
∵tan30°=
,∴
=
.
∴DE=
x
∵四边形ACED是矩形,
∴AC=DE=
x,CE=AD=18.
在Rt△ABC中,
∵tan60°=
,∴
=
.
∴x=9.
∴BC=BE+CE=9+18=27(米).
在Rt△BDE中,
∵tan30°=
| BE |
| DE |
| x |
| DE |
| 1 | ||
|
∴DE=
| 3 |
∵四边形ACED是矩形,
∴AC=DE=
| 3 |
在Rt△ABC中,
∵tan60°=
| BC |
| AC |
| x+18 | ||
|
| 3 |
∴x=9.
∴BC=BE+CE=9+18=27(米).
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
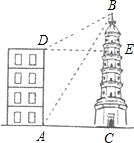 如图,小明想测量塔BC的高度.他在楼底A处测得塔顶B的仰角为60°;爬到楼顶D处测得大楼AD的高度为18米,同时测得塔顶B的仰角为30°,求塔BC的高度.
如图,小明想测量塔BC的高度.他在楼底A处测得塔顶B的仰角为60°;爬到楼顶D处测得大楼AD的高度为18米,同时测得塔顶B的仰角为30°,求塔BC的高度.

