题目内容
下面是芩芩用换元法解方程2(x+1)2+3(x+1)(x-2)-2(x-2)2=0的解答过程,请你判断是否正确.若有错误,请按上述思路求出正确答案.解:设x+1=m,x-2=n,则原方程可化为:2m2+3mn-2n2=0,
即a=2,b=3n,c=-2n2.
∴m=
3n±
| ||
| 2 |
| 3n±5n |
| 2 |
即 m1=4n,m2=-n.
所以有x+1=4(x-2)或x+1=-(x-2),
∴x1=3,x2=
| 1 |
| 2 |
分析:芩芩在运用一元二次方程的求根公式求根时出现错误.设x+1=m,x-2=n,利用换元法把原方程转化为:2m2+3mn-2n2=0,然后利用一元二次方程的求根公式解得m1=
n,m2=-2n,再转化为关于x的方程x+1=
(x-2)或x+1=-2(x-2),解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:该解答有错误.正确解答如下:
设x+1=m,x-2=n,则原方程可以为:2m2+3mn-2n2=0
即a=2,b=3n,c=-2n2
∴m=
=
,
∴m1=
n,m2=-2n,
∴x+1=
(x-2)或x+1=-2(x-2)
∴x1=-4,x2=1.
设x+1=m,x-2=n,则原方程可以为:2m2+3mn-2n2=0
即a=2,b=3n,c=-2n2
∴m=
-3n±
| ||
| 2×2 |
| -3n±5n |
| 4 |
∴m1=
| 1 |
| 2 |
∴x+1=
| 1 |
| 2 |
∴x1=-4,x2=1.
点评:本题考查了运用换元法解方程的方法:用一个字母代替一个代数式,把高次方程转化为一元二次方程或一元一次方程;也考查了一元二次方程的求根公式.

练习册系列答案
相关题目
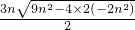 =
=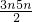
 .
. =
=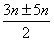

 =
=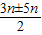
 .
.