题目内容
如图,已知抛物线y=ax2+2x+c的顶点为A(―1,―4),与y轴交于点B,与x轴负半轴交于点C.

(1)求这条抛物线的函数关系式;
(2)点P为第三象限内抛物线上的一动点,连接BC、PC、PB,求△BCP面积的最大值,并求出此时点P的坐标;
(3)点E为抛物线上的一点,点F为x轴上的一点,若四边形ABEF为平行四边形,请直接写出所有符合条件的点E的坐标.

(1)求这条抛物线的函数关系式;
(2)点P为第三象限内抛物线上的一动点,连接BC、PC、PB,求△BCP面积的最大值,并求出此时点P的坐标;
(3)点E为抛物线上的一点,点F为x轴上的一点,若四边形ABEF为平行四边形,请直接写出所有符合条件的点E的坐标.
(1)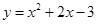 (2)
(2)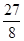 ,P(
,P(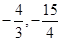 )
)
(3)(――1, 1)、(―1, 1)
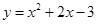 (2)
(2)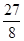 ,P(
,P(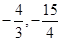 )
) (3)(――1, 1)、(―1, 1)
试题分析:(1)因为y=ax2+2x+c的顶点为A(―1,―4)
所以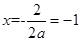 ,解得
,解得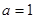
将A(―1,―4)代入y=ax2+2x+c
所以c=-3
所以该函数解析式为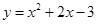
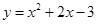
(2)如图,连接OP,

设点P(m,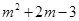 ),(―3<m<0)
),(―3<m<0)
∴S△PBC=S△OPC+S△OPB―S△BOC
=×3×( )+×3×(―m)―×3×3
)+×3×(―m)―×3×3
=―m―m
=―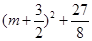
∴当m=―,即P(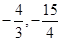 )
)
∴S△PBC有最大值为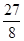 .
.
(3)抛物线y=ax2+2x+c与y轴交于点B,与x轴交于点C、D
所以B(0,-3),C(-3,0),D(1,0)
因为点E为抛物线上的一点,点F为x轴上的一点
若四边形ABEF为平行四边形
则E可为(――1, 1)、(―1, 1)
本题涉及了二次函数的解析式和几何意义,该题是常考题,主要考查学生对二次函数解析式系数与图像的关系,明确在直角坐标系中几何图形的意义。
所以
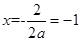 ,解得
,解得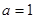
将A(―1,―4)代入y=ax2+2x+c
所以c=-3
所以该函数解析式为
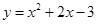
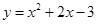
(2)如图,连接OP,

设点P(m,
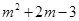 ),(―3<m<0)
),(―3<m<0)∴S△PBC=S△OPC+S△OPB―S△BOC
=×3×(
 )+×3×(―m)―×3×3
)+×3×(―m)―×3×3=―m―m
=―
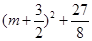
∴当m=―,即P(
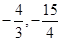 )
)∴S△PBC有最大值为
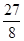 .
.(3)抛物线y=ax2+2x+c与y轴交于点B,与x轴交于点C、D
所以B(0,-3),C(-3,0),D(1,0)
因为点E为抛物线上的一点,点F为x轴上的一点
若四边形ABEF为平行四边形
则E可为(――1, 1)、(―1, 1)
本题涉及了二次函数的解析式和几何意义,该题是常考题,主要考查学生对二次函数解析式系数与图像的关系,明确在直角坐标系中几何图形的意义。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
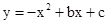 经过A
经过A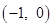 、C(0,4)两点,与x轴的另一交点是B.
、C(0,4)两点,与x轴的另一交点是B.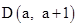 在第一象限的抛物线上,求点D关于直线BC的对称点
在第一象限的抛物线上,求点D关于直线BC的对称点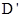 的坐标;
的坐标;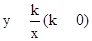 的图象经过点E,点
的图象经过点E,点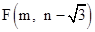 在此反比例函数图象上,求
在此反比例函数图象上,求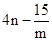 的值.
的值.
 .
. x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
 )三点.
)三点.

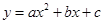
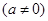 中的
中的 满足下表:
满足下表:
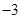
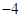
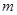
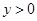 时的
时的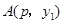 ,
,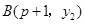 两点都在该函数图象上,且
两点都在该函数图象上,且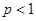 ,试比较
,试比较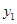 与
与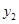 的大小.
的大小.