题目内容
已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= 。
2525
此题需把a1+a2+a3+…a100变形为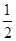 (a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1),再把a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100代入即可.
(a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1),再把a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100代入即可.
解:∵a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,
∴a1+a2+a3+…a100=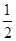 (a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1)=
(a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1)=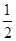 (1+2+3+…+100)=
(1+2+3+…+100)=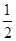 ×5050=2525.
×5050=2525.
故填:2525.
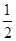 (a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1),再把a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100代入即可.
(a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1),再把a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100代入即可.解:∵a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,
∴a1+a2+a3+…a100=
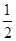 (a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1)=
(a1+a2+a2+a3+a3+a4+,…,a99+a100+a100+a1)=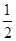 (1+2+3+…+100)=
(1+2+3+…+100)=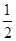 ×5050=2525.
×5050=2525.故填:2525.

练习册系列答案
相关题目
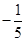 的相反数是( )
的相反数是( )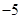
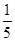

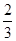 的值为
的值为 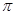 的近似值在
的近似值在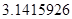 与
与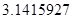 之间,若精确到
之间,若精确到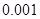 ,则
,则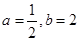 时,求
时,求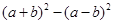 的值。(8分)
的值。(8分)