题目内容
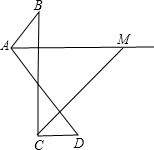 已知如图,∠B=32°,∠D=38°,AM、CM分别平分∠BAD和∠BCD.
已知如图,∠B=32°,∠D=38°,AM、CM分别平分∠BAD和∠BCD.(1)求∠M的大小.
(2)当∠B、∠D为任意角时,试探索∠M与∠B、∠D间的数量关系,并说明理由.
分析:(1)如图,根据外角的性质定理可知∠5=∠1+∠B,∠6=∠4+∠D,∠BED=2∠1+∠B=2∠4+∠D,再根据三角形的内角和定理和四边形的内角和定理,可得180°-∠5+180°-∠6+∠BED+∠M=360°,然后通过等量代换即可推出∠M的度数,
(2)根据(1)的推理思路即可推出∠M=
(∠B+∠D).
(2)根据(1)的推理思路即可推出∠M=
| 1 |
| 2 |
解答: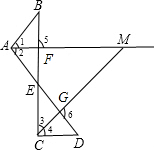 解:(1)如图,∵AM、CM分别平分∠BAD和∠BCD,
解:(1)如图,∵AM、CM分别平分∠BAD和∠BCD,
∴∠5=∠1+∠B,∠6=∠4+∠D,∠BED=2∠1+∠B=2∠4+∠D,
∵四边形FEGM的内角和为360°,
∴180°-∠5+180°-∠6+∠BED+∠M=360°,
∴∠M=∠5+∠6-∠BED=∠1+∠B+∠4+∠D-[(2∠1+∠B)+(2∠4+∠D)]×
=(∠B+
∠D)×
,
∵∠B=32°,∠D=38°,
∴∠M=35°;
(2)如图,∵AM、CM分别平分∠BAD和∠BCD,
∵∠5是△ABF的外角,∠6是△CDG的外角,∠BED是△CDE的外角,
∴∠5=∠1+∠B,∠6=∠4+∠D,∠BED=2∠1+∠B=2∠4+∠D(三角形的外角等于与它不相邻的两个内角的和)
∵四边形FEGM的内角和为360°,
∴180°-∠5+180°-∠6+∠BED+∠AMC=360°,
∴∠M=∠5+∠6-∠BED=∠1+∠B+∠4+∠D-[(2∠1+∠B)+(2∠4+∠D)]×
=(∠B+∠D)×
,
即∠M=
(∠B+∠D).
 解:(1)如图,∵AM、CM分别平分∠BAD和∠BCD,
解:(1)如图,∵AM、CM分别平分∠BAD和∠BCD,∴∠5=∠1+∠B,∠6=∠4+∠D,∠BED=2∠1+∠B=2∠4+∠D,
∵四边形FEGM的内角和为360°,
∴180°-∠5+180°-∠6+∠BED+∠M=360°,
∴∠M=∠5+∠6-∠BED=∠1+∠B+∠4+∠D-[(2∠1+∠B)+(2∠4+∠D)]×
| 1 |
| 2 |
∠D)×
| 1 |
| 2 |
∵∠B=32°,∠D=38°,
∴∠M=35°;
(2)如图,∵AM、CM分别平分∠BAD和∠BCD,
∵∠5是△ABF的外角,∠6是△CDG的外角,∠BED是△CDE的外角,
∴∠5=∠1+∠B,∠6=∠4+∠D,∠BED=2∠1+∠B=2∠4+∠D(三角形的外角等于与它不相邻的两个内角的和)
∵四边形FEGM的内角和为360°,
∴180°-∠5+180°-∠6+∠BED+∠AMC=360°,
∴∠M=∠5+∠6-∠BED=∠1+∠B+∠4+∠D-[(2∠1+∠B)+(2∠4+∠D)]×
| 1 |
| 2 |
| 1 |
| 2 |
即∠M=
| 1 |
| 2 |
点评:本题主要考查三角形的内角和定理、四边形的内角和定理、角平分线的性质、外角的性质,关键在于熟练运用个性质定理推出相关角之间的关系.

练习册系列答案
相关题目
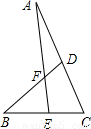
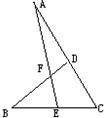 12、已知如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
12、已知如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( ) 已知如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于
已知如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于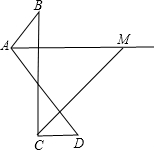 已知如图,∠B=32°,∠D=38°,AM、CM分别平分∠BAD和∠BCD.
已知如图,∠B=32°,∠D=38°,AM、CM分别平分∠BAD和∠BCD.