Question

【题目】如图，四边形是矩形 ,是延长线上的一点，是上一点，;若,则 = ________ .

Answer 1

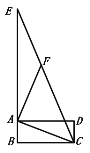
【答案】

【解析】由矩形的性质得出∠BCD=90°，AB∥CD，AD∥BC，证出∠FEA=∠ECD，∠DAC=∠ACB=21°，由三角形的外角性质得出∠ACF=2∠FEA，设∠ECD=x，则∠ACF=2x，∠ACD=3x，由互余两角关系得出方程，解方程即可．

∵四边形ABCD是矩形，

∴∠BCD=90°，AB∥CD，AD∥BC，

∴∠FEA=∠ECD，∠DAC=∠ACB=21°，

∵∠ACF=∠AFC，∠FAE=∠FEA，

∴∠ACF=2∠FEA，

设∠ECD=x，则∠ACF=2x，

∴∠ACD=3x，

∴3x+21°=90°，

解得：x=23°.

故答案为：23°．