题目内容
直线y=-2x+4和直线y=x-2与y轴围成的三角形的面积是
- A.6
- B.8
- C.10
- D.12
A
分析:本题需先求出两直线与坐标轴交点的坐标,然后再根据三角形的面积公式求出所围三角形的面积.
解答:直线y=-2x+4中,令y=0,则x=2;令x=0,则y=4;
因此直线y=-2x+4与坐标轴的交点为(2,0),(0,4);
同理可求得直线y=x-2与坐标轴的交点为(2,0),(0,-2).

因此直线y=-2x+4和直线y=x-2与y轴围成的三角形的面积是:S= ×6×2=6.
×6×2=6.
故选A.
点评:本题考查了两条直线相交或平行问题,正确求出两直线与坐标轴的交点是解决本题的关键,比较简单.
分析:本题需先求出两直线与坐标轴交点的坐标,然后再根据三角形的面积公式求出所围三角形的面积.
解答:直线y=-2x+4中,令y=0,则x=2;令x=0,则y=4;
因此直线y=-2x+4与坐标轴的交点为(2,0),(0,4);
同理可求得直线y=x-2与坐标轴的交点为(2,0),(0,-2).

因此直线y=-2x+4和直线y=x-2与y轴围成的三角形的面积是:S=
 ×6×2=6.
×6×2=6.故选A.
点评:本题考查了两条直线相交或平行问题,正确求出两直线与坐标轴的交点是解决本题的关键,比较简单.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
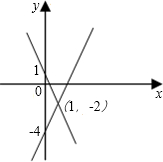 如图,直线y=2x-4和直线y=-3x+1交于一点,则方程组
如图,直线y=2x-4和直线y=-3x+1交于一点,则方程组
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
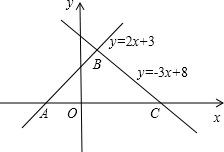 求直线y=2x+3和y=-3x+8与x轴所围成的面积.
求直线y=2x+3和y=-3x+8与x轴所围成的面积.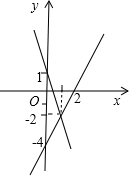 如图,直线y=2x-4和直线y=-3x+1交于一点,则方程组
如图,直线y=2x-4和直线y=-3x+1交于一点,则方程组