题目内容
如图,∠1+∠2=180°,∠3=108°,则∠4的度数是
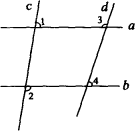
[ ]
A.72°
B.80°
C.82°
D.108°
答案:A

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
题目内容
如图,∠1+∠2=180°,∠3=108°,则∠4的度数是

A.72°
B.80°
C.82°
D.108°

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案