题目内容
(2013•静安区二模)在△ABC中,∠A=40°,△ABC绕点A旋转后点C落在边AB上的点C′,点B落到点B′,如果点C、C′、B′在同一直线上,那么∠B的度数是
30°
30°
.分析:作出图形,根据旋转的性质可得AC=AC′,∠B′AC′=∠BAC,根据等腰三角形两底角相等求出∠AC′C,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠AB′C,根据旋转的性质可得∠ABC=∠AB′C′,从而得解.
解答: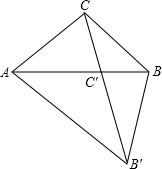 解:如图,∵△AB′C′是△ABC旋转得到,
解:如图,∵△AB′C′是△ABC旋转得到,
∴AC=AC′,∠B′AC′=∠BAC=40°,
∴∠AC′C=
(180°-∠BAC)=
(180°-40°)=70°,
∵点C的对应点C′落在AB上,
∴∠AB′C′=∠AC′C-∠B′AC′=70°-40°=30°.
故答案为:30°.
 解:如图,∵△AB′C′是△ABC旋转得到,
解:如图,∵△AB′C′是△ABC旋转得到,∴AC=AC′,∠B′AC′=∠BAC=40°,
∴∠AC′C=
| 1 |
| 2 |
| 1 |
| 2 |
∵点C的对应点C′落在AB上,
∴∠AB′C′=∠AC′C-∠B′AC′=70°-40°=30°.
故答案为:30°.
点评:本题考查了旋转的性质,等腰三角形两底角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 (2013•静安区二模)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )
(2013•静安区二模)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )