题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
把(600,400),(700,300)两点的坐标分别代入y=kx+b,得 |
(2) |
①s=xy-500y=x(-x+1000)-500(-x+1000),s=-x2+1500x-500000(500≤x≤800) ②s=-x2+1500x-500000=-(x-750)2+62500,当x=750时,S最大=62500.此时,y=-x+1000=-750+1000=250(件).故当销售单价定为750元时,该公司获得最大毛利润是62500元,此时销售量是250件 |

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

 27、某公司试销一种成本单价为400元/件的新产品,规定试销时的销售单价不底于成本价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似的看作一次函数y=kx+b的关系.
27、某公司试销一种成本单价为400元/件的新产品,规定试销时的销售单价不底于成本价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似的看作一次函数y=kx+b的关系.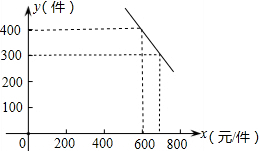 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.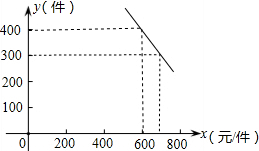 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件.试销时,发现销售量y(件)与销售价x(元/件)的关系可近似看作一次函数y=kx+b(k≠0),如图所示.