题目内容
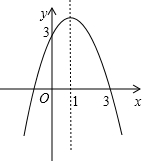
已知二次函数y=-x2+4x．
（1）用配方法把该函数化为y=a（x-h）2+k（其中a、h、k都是常数且a≠0）的形式，并指出；
（2）求这个函数图象与x轴的交点坐标．
（3）求出当x取何值时，y随着x的增大而减小；当x取何值时，y＞0，当x取何值时，y＜0？
（1）用配方法把该函数化为y=a（x-h）2+k（其中a、h、k都是常数且a≠0）的形式，并指出；
（2）求这个函数图象与x轴的交点坐标．
（3）求出当x取何值时，y随着x的增大而减小；当x取何值时，y＞0，当x取何值时，y＜0？
（1）y=-x2+4x=-（x2一4x+4-4）=-（x一2）2+4，（3分）
∴对称轴为：直线x=2，（1分）
顶点坐标：（2，4）；（1分）
（2）二次函数y=-x2+4x与x轴的交点就是方程-x2+4x=0的两根．
解方程-x2+4x=0，得x1=0，x2=4，
∴图象与x轴的交点坐标为：（0，0）与（4，0）；（2分）
（3）由图象可知，①当x≥2时，y随着x的增大而减小；
②当0＜x＜4时，y＞0；
③当x＞4或x＜0时，y＜0．
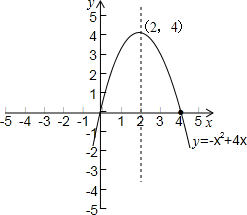
∴对称轴为：直线x=2，（1分）
顶点坐标：（2，4）；（1分）
（2）二次函数y=-x2+4x与x轴的交点就是方程-x2+4x=0的两根．
解方程-x2+4x=0，得x1=0，x2=4，
∴图象与x轴的交点坐标为：（0，0）与（4，0）；（2分）
（3）由图象可知，①当x≥2时，y随着x的增大而减小；
②当0＜x＜4时，y＞0；
③当x＞4或x＜0时，y＜0．
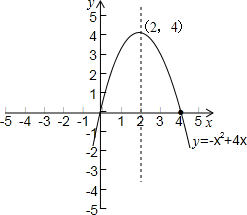
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
