题目内容
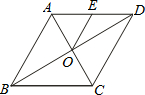（2012•丹东）如图，菱形ABCD的周长为24cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长等于（ ）分析：先求出菱形的边长AB，再根据菱形的对角线互相平分判断出OE是△ABD的中位线，然后根据三角形的中位线等于第三边的一半解答．
解答：解：∵菱形ABCD的周长为24cm，
∴边长AB=24÷4=6cm，
∵对角线AC、BD相交于O点，
∴BO=DO，
又∵E是AD的中点，
∴OE是△ABD的中位线，
∴OE=
AB=
×6=3cm．
故选A．
∴边长AB=24÷4=6cm，
∵对角线AC、BD相交于O点，
∴BO=DO，
又∵E是AD的中点，
∴OE是△ABD的中位线，
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查了菱形的对角线互相平分的性质，三角形的中位线定理，是基础题，求出OE等于菱形边长的一半是解题的关键．
练习册系列答案
相关题目
（2012•丹东）如图，在△ABC中，∠BAC=30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且
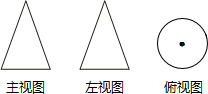（2012•丹东）如图是一个几何体的三视图，则这个几何体是（ ）
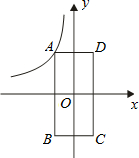（2012•丹东）如图，点A是双曲线y=
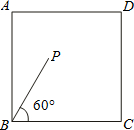（2012•丹东）如图，边长为6的正方形ABCD内部有一点P，BP=4，∠PBC=60°，点Q为正方形边上一动点，且△PBQ是等腰三角形，则符合条件的Q点有