��Ŀ����
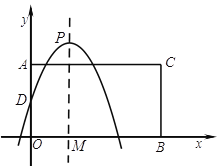
����Ŀ����ͼ, ��ƽ��ֱ������ϵ��,��A��B�ֱ���![]() ��������,
��������, ![]() ����������������,
����������������, ![]() ��
�� ![]() ����AO��BOΪ�ڱ߹������AOBC��������
����AO��BOΪ�ڱ߹������AOBC��������![]() ��
��![]() ���ڵ�D��PΪ���㣬PM��
���ڵ�D��PΪ���㣬PM��![]() ���ڵ�M��
���ڵ�M��
��1����![]() ��
�� ![]() �ij�(������ú�
�ij�(������ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
��2����![]() ʱ,��������ߵı���ʽ��
ʱ,��������ߵı���ʽ��
��3���ڵ�![]() �������˶������У�
�������˶������У�
��������![]() �ǵ���������,�������������������
�ǵ���������,�������������������![]() ��ֵ��
��ֵ��
�ڵ���A����ֱ��DP�ĶԳƵ�![]() ǡ������������
ǡ������������![]() ��ͼ����ʱ����ֱ��д��
��ͼ����ʱ����ֱ��д��![]() ��ֵ��
��ֵ��
���𰸡���1��OD��Ϊk��PM�ij�Ϊk+3��
��2���������ߵı���ʽΪ![]() ��
��
��3��������������![]() ��ֵΪ
��ֵΪ![]() �� 6����
�� 6����![]()
��![]() ��ֵΪ
��ֵΪ![]() .
.
����������1����D��y=��x2+3x+k�ϣ�����y���ϣ���y=0�����D���꣬���������߶��㹫ʽ��������ɣ�
��2������k��ʾ����صĵ�����꣬����PM=BM�������̼��ɣ�
��3��������k��ʾ����صĵ�����꣬���ݡ�ADP�ǵ��������Σ������������AD=AP��DA=DP��PA=PD���㣻
���ɵ�P��D�������ֱ��PD����ʽ������PD��AA�䣬��A��0��2k����ȷ����AA�����ʽ���̶�������㣬�����A������꼴�ɣ�
�⣺��1����x=0������![]() ����
����![]() ����
����![]() ��
��
��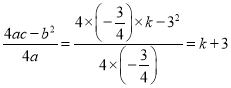 ����
����![]() ��
��
��2����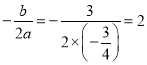 ����
����![]() ,
, ![]() ��
��
�֡�![]() ��
�� ![]() ����
����![]() �����
�����![]() ��
��
��������ߵı���ʽΪ![]() ��
��
��3����
����P�ھ���AOBC�ⲿʱ
��ͼ��ʾ��
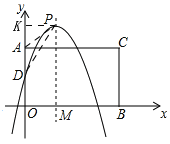
��P��PK��OA�ڵ�K����AD=APʱ,
��AD=AO-DO=2k-k=k��
��AD=AP =k��KA=KO-AO=PM-AO= ![]()
KP=OM=2����Rt��KAP�� ![]()
��![]() �����
�����![]() ��
��
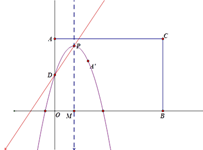
����P�ھ���AOBC�ڲ�ʱ
��PD=APʱ,��ͼ��ʾ��

��P��PH��OA��H��
AD=k��HD=![]() ��
�� ![]()
�֡�HO=PM= ![]() ��
��
��![]() �����
�����![]() ��
��
��DP=DAʱ,��ͼ��ʾ��

��D��PQ��PM��Q��
PQ=PM-QM=PM-OD= ![]()
DQ=OM=2��DP=DA=k��
��Rt��DQP�� ![]() ��
��
��![]() ��
��
��![]() ��
��
���㾦�������Ƕ��κ����ۺ��⣬��Ҫ�����˶��κ�������ʽ��ȷ����ƽ������ϵ�����߶εij������������ε����ʣ�ȷ������������ʽ�ǽⱾ��Ĺؼ�. �⣨3���DZ�����ѵ�.

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�����Ŀ��ijУ��ȥ�Ϫ��ij���㴺�Σ�����������ѧ���Ƴ����շѱ����£�
����m | 0��m��100 | 100��m��200 | m��200 |
�շѱ���Ԫ/�ˣ� | 90 | 80 | 70 |
��֪��У���꼶�μӴ���ѧ����������100�ˣ����꼶�μӴ���ѧ����������100�ˣ������㣬�������꼶�ֱ����Ź��軨��17700Ԫ���������꼶��������ֻ�軨��14700Ԫ��
��1�������꼶�μӴ���ѧ������֮�ͳ���200����Ϊʲô��
��2�������꼶�μӴ���ѧ�����ж����ˣ�