Question

【题目】如图，在△ABC中，CE平分∠ACB，CE⊥AB于点 E，过 E作 ED∥AC交 BC于点 D，过 D作 DF⊥AB于点 F.

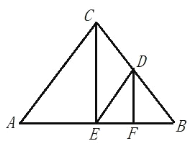
（1）若∠ACE=40°，求∠EDC的度数.

（2）判断∠EDF与∠BDF是否相等，并说明理由.

Answer 1

【答案】（1）100；（2）相等，理由见解析．

【解析】

（1）由角平分线的性质结合平行线的性质可求解；
（2）由平行线的性质可求∠BCE=∠BDF=40，由平角的定义可求得∠EDF=∠BDF．

（1）∵CE平分∠ACB，
∴∠ACE=∠BCE=40∠ACB，
∴∠ACB=80，
∵AC∥DE，
∴∠ACB+∠EDC=180，
∴∠EDC=180-∠ACB=180-80＝100；
（2）∠EDF=∠BDF，
理由如下：
∵DF⊥AB，CE⊥AB，
∴CE∥DF，
∴∠BCE=∠BDF=40，
∴∠EDF=180-∠CDE-∠BDF=40，
∴∠EDF=∠BDF．