题目内容
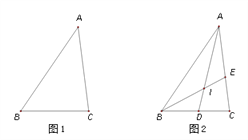
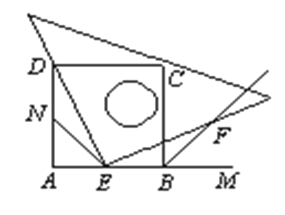
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
⑵请你证明上述两种猜想?
【答案】⑴①DE=EF;②NE=BF;(2)证明见解析
【解析】试题分析:(1)根据图形可以得到DE=EF,NE=BF;(2)根据正方形的性质及N,E分别为AD,AB的中点可得DN=EB,再根据角平分线的性质及AN=AE可得∠DNE=∠EBF=135°,再根据同角的余角相等证得∠NDE=∠BEF,即可证得△DNE≌△EBF,从而证得结论.
试题解析:
⑴①DE=EF;②NE=BF。
(2)证明:∵四边形ABCD是正方形,N,E分别为AD,AB的中点,
∴DN=EB
∵BF平分∠CBM,AN=AE
∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°∠BEF+∠DEA=90°
∴∠NDE=∠BEF
∴△DNE≌△EBF
∴ DE=EF,NE=BF

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目