题目内容
【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
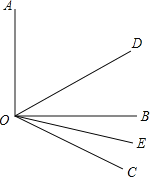
【答案】(1)∠COD =60°;(2)∠DOE=45°;(3)∠DOE=![]() α.
α.
【解析】
(1)根据角平分线的定义即可得到结论;
(2)根据角平分线的定义可以得到![]() 然后根据∠DOE=∠COD-∠COE即可求解;
然后根据∠DOE=∠COD-∠COE即可求解;
(3)根据角平分线的定义可以得到![]() 然后根据∠DOE=∠COD-∠COE即可求解.
然后根据∠DOE=∠COD-∠COE即可求解.
(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=120°,
∵OD平分∠AOC,
∴∠COD=![]() ∠AOC=60°;
∠AOC=60°;
(2)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=∠AOB+∠BOC=90°+3,0°=120°
又∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=
∠AOC=![]() ×120°=60°,
×120°=60°,
∠COE=![]() ∠BOC=
∠BOC=![]() ×30°=15°,
×30°=15°,
∴∠DOE=∠COD-∠COE=60°-15°=45°;
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=
∠AOC=![]() (α+β),
(α+β),
∠COE=![]() ∠BOC=
∠BOC=![]() β,
β,
∴∠DOE=∠COD-∠COE=![]() (α+β)-
(α+β)-![]() β=
β=![]() α+
α+![]() β-
β-![]() β=
β=![]() α.
α.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目