题目内容
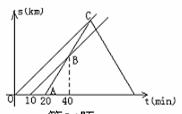
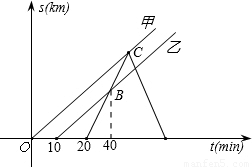
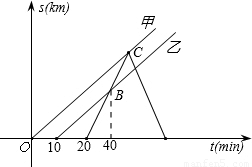
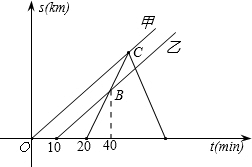 甲乙两车先后都以60km/h的速度从M地将一批物品运往N地.两车出发后,发货站发现甲车遗漏一件物品,遂派丙车将遗漏物品送达甲车.丙车完成任务后,即沿原路返回(物品交接时间忽略不计).如图表示三辆车离M地的距离s(km)随时间t(min)变化的图象.
甲乙两车先后都以60km/h的速度从M地将一批物品运往N地.两车出发后,发货站发现甲车遗漏一件物品,遂派丙车将遗漏物品送达甲车.丙车完成任务后,即沿原路返回(物品交接时间忽略不计).如图表示三辆车离M地的距离s(km)随时间t(min)变化的图象.请根据图象进行以下探究:
信息读取
(1)说明图象中点B的实际意义;
图象理解
(2)甲车出发多长时间后被丙车追上?此时追及点距M地多远?
问题解决
(3)丙车与乙车在距离M地多远处迎面相遇?
分析:(1)丙车在甲车出发后追上乙车;
(2)设甲车出发xh被丙车追上,列出关系式,解出x;
(3)设丙车从返回到遇上乙车用了yh,算出乙车离M地的距离,列出关系式,求出y.
(2)设甲车出发xh被丙车追上,列出关系式,解出x;
(3)设丙车从返回到遇上乙车用了yh,算出乙车离M地的距离,列出关系式,求出y.
解答:解:(1)丙车在甲车出发后40min时追上乙车,
此时丙、乙两车距离M地30km;
(2)由图象可知,乙车行驶了30分钟就被丙追上,这时乙行驶的路程是:60×
=30(km),
丙行驶20分钟就追上了乙,故丙车速度是:30÷
=90(km/h),
设甲车出发xh被丙车追上,列方程得60x=90(x-
)
解得x=1,
此时,60x=60×1=60.
答:甲车出发1小时被丙车追上,此时追及点距M地60km.
(3)由(2)可知,丙车追上甲车时行驶了60km,此时乙车行驶了50min,离M地50km,
设丙车从返回到遇上乙车用了yh,列方程得(60+90)y=60-50,
解得y=
h,即y=4min,即乙车又走了4千米,50+60×
=54km,即相遇时距离M地54km.
答:丙车与乙车在距离M地54km处迎面相遇.
此时丙、乙两车距离M地30km;
(2)由图象可知,乙车行驶了30分钟就被丙追上,这时乙行驶的路程是:60×
| 1 |
| 2 |
丙行驶20分钟就追上了乙,故丙车速度是:30÷
| 20 |
| 60 |
设甲车出发xh被丙车追上,列方程得60x=90(x-
| 1 |
| 3 |
解得x=1,
此时,60x=60×1=60.
答:甲车出发1小时被丙车追上,此时追及点距M地60km.
(3)由(2)可知,丙车追上甲车时行驶了60km,此时乙车行驶了50min,离M地50km,
设丙车从返回到遇上乙车用了yh,列方程得(60+90)y=60-50,
解得y=
| 1 |
| 15 |
| 1 |
| 15 |
答:丙车与乙车在距离M地54km处迎面相遇.
点评:本题主要考查一次函数的应用,会用一次函数研究实际问题,具备在直角坐标系中的读图能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
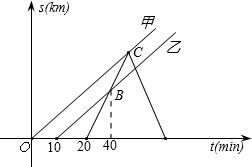 甲乙两车先后都以60km/h的速度从M地将一批物品运往N地.两车出发后,发货站发现甲车遗漏一件物品,遂派丙车将遗漏物品送达甲车.丙车完成任务后,即沿原路返回(物品交接时间忽略不计).如图表示三辆车离M地的距离s(km)随时间t(min)变化的图象.
甲乙两车先后都以60km/h的速度从M地将一批物品运往N地.两车出发后,发货站发现甲车遗漏一件物品,遂派丙车将遗漏物品送达甲车.丙车完成任务后,即沿原路返回(物品交接时间忽略不计).如图表示三辆车离M地的距离s(km)随时间t(min)变化的图象.