题目内容
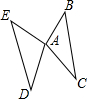
如图，已知△ABC≌△ADE，BC的边长线交AD于F，交AE于G，∠ACB=105°，∠CAD=10°，∠ADE=25°，求∠DFB和∠AGB的度数．
∵△ABC≌△ADE，
∴∠ACB=∠AED，∠ABC=∠ADE，∠CAB=∠EAD．
∵∠ADE=25°，
∴∠ABC=∠ADE=25°．
∵∠ACB=105°，
∴∠CAB=180°-105°-25°=50°．
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°．
∠AGB=∠ACB-∠GAC=105°-50°-10°=45°．
∴∠ACB=∠AED，∠ABC=∠ADE，∠CAB=∠EAD．
∵∠ADE=25°，
∴∠ABC=∠ADE=25°．
∵∠ACB=105°，
∴∠CAB=180°-105°-25°=50°．
∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°．
∠AGB=∠ACB-∠GAC=105°-50°-10°=45°．
练习册系列答案
阅读快车系列答案
相关题目
