题目内容
如图1,经过原点O的抛物线y=ax2+bx(a、b为常数,a≠0)与x轴相交于另一点A(3,0).直线l:y=x在第一象限内和此抛物线相交于点B(5,t),与抛物线的对称轴相交于点C.

(1)求抛物线的解析式;
(2)在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;
(3)直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;
(4)在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.
练习册系列答案
相关题目





 B.
B. 
 D.
D. 


 B.
B.  C.
C.  D.
D. 
 ≈1.414,
≈1.414,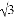 ≈1.732)
≈1.732)