题目内容
某校为了了解学生的学习负担情况,调查了九年级学生每天课外作业所花时间的情况,从每班抽取5名学生作为样本,按A、B、C、D四个类别进行统计.并将统计结果绘制成以下两幅不完整的统计图,请你结合图中信息解答下列问题:(说明:A类:60分钟以下;B类:60分钟-74分钟;C类75分钟-89分钟;D类:90分钟-100分钟)
(1)A类学生的人数为
(2)扇形统计图中C类学生的人数所占扇形圆心角的度数为
(3)若该校九年级共有学生500人,请你估计全年级中A类和B类的学生共有多少人.
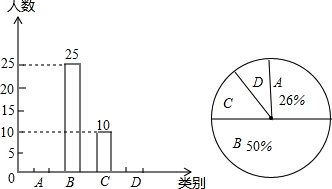
(1)A类学生的人数为
13
13
请补全条形统计图;(2)扇形统计图中C类学生的人数所占扇形圆心角的度数为
72°
72°
,D类学生的人数占抽样总人数的百分比为4%
4%
;(3)若该校九年级共有学生500人,请你估计全年级中A类和B类的学生共有多少人.

分析:(1)先求出抽取的学生总数,再根据A类学生所占的百分比,求出A类学生的人数,再用总人数减去A、B、C三类学生的人数,即可得出D类学生的人数,从而补全条形统计图;
(2)用C类学生的人数所占的百分比乘以360°即可得出C类学生的人数所占扇形圆心角的度数;
用D类学生的人数除以总人数即可得出D类学生的人数占抽样总人数的百分比;
(3)用全年级的总人数乘以全年级A类和B类的学生人数所占的百分比,即可求出答案.
(2)用C类学生的人数所占的百分比乘以360°即可得出C类学生的人数所占扇形圆心角的度数;
用D类学生的人数除以总人数即可得出D类学生的人数占抽样总人数的百分比;
(3)用全年级的总人数乘以全年级A类和B类的学生人数所占的百分比,即可求出答案.
解答:解:(1)∵抽取的学生总数=25÷50%=50,
∴A类学生的人数=50×26%=13(人),
∴D类学生的人数是50-13-25-10=2(人),
补图如下:
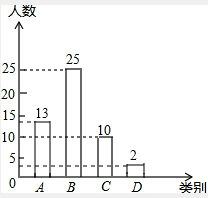
故答案为:13.
(2)C类学生的人数所占扇形圆心角的度数为
×360°=72°,
D类学生的人数占抽样总人数的百分比为
×100%=4%;
故答案为:72°,4%.
(3)根据题意得:
全年级A类和B类的学生人数=500×(26%+50%)=380(人),
答:全年级中A类和B类的学生共有380人.
∴A类学生的人数=50×26%=13(人),
∴D类学生的人数是50-13-25-10=2(人),
补图如下:

故答案为:13.
(2)C类学生的人数所占扇形圆心角的度数为
| 10 |
| 50 |
D类学生的人数占抽样总人数的百分比为
| 2 |
| 50 |
故答案为:72°,4%.
(3)根据题意得:
全年级A类和B类的学生人数=500×(26%+50%)=380(人),
答:全年级中A类和B类的学生共有380人.
点评:本题考查了条形统计图和扇形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据,扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
中考前夕,某校为了了解初三年级480名学生的数学学习情况,特组织了一次检测.教师随机抽取了一部分学生的检测成绩进行统计分析,绘制成下表:
初三年级数学检测质量分析抽样统计表
| 样本容量 | 平均分 | 及格率 | 优秀率 | 后进率 | 最高分 | 最低分 | 全距 | 标准差 | |
| 87.5 | 80% | 2% | 120 | 29 | 91 | ||||
| 分数段统计 | |||||||||
| 分数段 | 0-35.5 | 36-47.5 | 48-59.5 | 60-71.5 | 72-83.5 | 84-95.5 | 96-107.5 | 108-119.5 | 120 |
| 频数 | 1 | 2 | 3 | 9 | 14 | 10 | 6 | 1 | |
| 频率 | 0.02 | 0.04 | 0.06 | 0.08 | 0.28 | 0.20 | 0.12 | 0.02 | |
(1)仔细观察上表,填出表中空格处的相应数据;
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(3)根据表中相关统计量及相应数据,结合你所学的统计知识,选择两个方面对这次检测的总体情况作出合理分析.
中考前夕,某校为了了解初三年级480名学生的数学学习情况,特组织了一次检测.教师随机抽取了一部分学生的检测成绩进行统计分析,绘制成下表:
初三年级数学检测质量分析抽样统计表
注:72分(含72分)以上为“及格”;96分(含96分)以上为“优秀”;36分(不含36分)以下为“后进”,全距是“最高分”与“最低分”之差.
(1)仔细观察上表,填出表中空格处的相应数据;
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(3)根据表中相关统计量及相应数据,结合你所学的统计知识,选择两个方面对这次检测的总体情况作出合理分析.
初三年级数学检测质量分析抽样统计表
| 样本容量 | 平均分 | 及格率 | 优秀率 | 后进率 | 最高分 | 最低分 | 全距 | 标准差 | |
| 87.5 | 80% | 2% | 120 | 29 | 91 | ||||
| 分数段统计 | |||||||||
| 分数段 | 0-35.5 | 36-47.5 | 48-59.5 | 60-71.5 | 72-83.5 | 84-95.5 | 96-107.5 | 108-119.5 | 120 |
| 频数 | 1 | 2 | 3 | 9 | 14 | 10 | 6 | 1 | |
| 频率 | 0.02 | 0.04 | 0.06 | 0.08 | 0.28 | 0.20 | 0.12 | 0.02 | |
(1)仔细观察上表,填出表中空格处的相应数据;
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(3)根据表中相关统计量及相应数据,结合你所学的统计知识,选择两个方面对这次检测的总体情况作出合理分析.
(2006•曲靖)中考前夕,某校为了了解初三年级480名学生的数学学习情况,特组织了一次检测.教师随机抽取了一部分学生的检测成绩进行统计分析,绘制成下表:
初三年级数学检测质量分析抽样统计表
注:72分(含72分)以上为“及格”;96分(含96分)以上为“优秀”;36分(不含36分)以下为“后进”,全距是“最高分”与“最低分”之差.
(1)仔细观察上表,填出表中空格处的相应数据;
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(3)根据表中相关统计量及相应数据,结合你所学的统计知识,选择两个方面对这次检测的总体情况作出合理分析.
初三年级数学检测质量分析抽样统计表
| 样本容量 | 平均分 | 及格率 | 优秀率 | 后进率 | 最高分 | 最低分 | 全距 | 标准差 | |
| 87.5 | 80% | 2% | 120 | 29 | 91 | ||||
| 分数段统计 | |||||||||
| 分数段 | 0-35.5 | 36-47.5 | 48-59.5 | 60-71.5 | 72-83.5 | 84-95.5 | 96-107.5 | 108-119.5 | 120 |
| 频数 | 1 | 2 | 3 | 9 | 14 | 10 | 6 | 1 | |
| 频率 | 0.02 | 0.04 | 0.06 | 0.08 | 0.28 | 0.20 | 0.12 | 0.02 | |
(1)仔细观察上表,填出表中空格处的相应数据;
(2)估计这480名学生本次检测成绩的中位数落在哪个分数段内;
(3)根据表中相关统计量及相应数据,结合你所学的统计知识,选择两个方面对这次检测的总体情况作出合理分析.
