题目内容
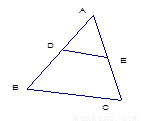
 如图△ABC中,DE∥AC交AB于E,DF∥AB交AC于F,
如图△ABC中,DE∥AC交AB于E,DF∥AB交AC于F,(1)如果AD是△ABC的角平分线,那么四边形AEDF是
菱形
菱形
形.请证明你的结论.(2)在(1)的条件下,给△ABC再添加一个条件:
∠BAC=90°(答案不唯一)
∠BAC=90°(答案不唯一)
,则四边形AEDF是正方形.(只填空,不要证明)分析:(1)由角平分线的性质与平行线的性质,可得∠EAD=∠DAF=∠ADE,进而可得AE=ED,由平行四边形的性质,可得答案;
(2)由(1)可知四边形AEFD是菱形,根据有一个角是90°的菱形是正方形填空即可.
(2)由(1)可知四边形AEFD是菱形,根据有一个角是90°的菱形是正方形填空即可.
解答:(1)菱形,
证明:∵DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形.
∵DE∥AC
∴∠1=∠3
又∵∠1=∠2°
∴∠2=∠3
∴AE=ED
∴□AEDF是菱形;
(2)∠BAC=90°,
理由如下:∵四边形AEDF是菱形,∠BAC=90°,
∴四边形AEDF是正方形.
证明:∵DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形.
∵DE∥AC
∴∠1=∠3
又∵∠1=∠2°
∴∠2=∠3
∴AE=ED
∴□AEDF是菱形;
(2)∠BAC=90°,
理由如下:∵四边形AEDF是菱形,∠BAC=90°,
∴四边形AEDF是正方形.
点评:本题考查特殊平行四边形:菱形、正方形的判定和性质,解题时注意从边的关系(相等、垂直)进行分析.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
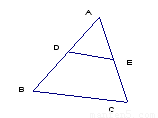
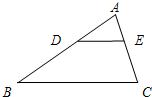 11、如图△ABC中,DE∥BC,AD:BD=1:2,则DE:BC=
11、如图△ABC中,DE∥BC,AD:BD=1:2,则DE:BC= (2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于
(2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于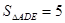 ,则
,则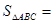
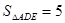 ,则
,则